Collections de l'Institut Henri Poincaré

Contenus

• Cu-Csi-001
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM1
• Cu-Csi-002
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM2
• Cu-Csi-003
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM3
• Cu-Csi-004
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM4
• Cu-Csi-005
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM5
• Cu-Csi-006
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM6
• Cu-Csi-007
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM7
• Cu-Csi-008
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM8
• Cu-Csi-009
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM9
• Cu-Csi-010
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM10
• Cu-Csi-011
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM11
• Cu-Csi-012
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM12
• Cu-Csi-013
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM13
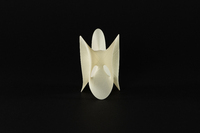• Cu-Csi-014
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM14
• Cu-Csi-015
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM15
• Cu-Csi-016
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM16
• Cu-Csi-017
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM17
• Cu-Csi-018
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM18
• Cu-Csi-019
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM19
• Cu-Csi-020
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM20
• Cu-Csi-021
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM21
• Cu-Csi-022
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM22
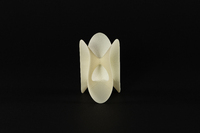• Cu-Csi-023
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM23
• Cu-Csi-024
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM24
• Cu-Csi-025
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM25
• Cu-Csi-026
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM26
• Cu-Csi-027
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM27
• Cu-Csi-028
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM28
• Cu-Csi-029
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM29
• Cu-Csi-030
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM30
• Cu-Csi-031
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM31
• Cu-Csi-032
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM32
• Cu-Csi-033
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM33
• Cu-Csi-034
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM34
• Cu-Csi-035
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM35
• Cu-Csi-036
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM36
• Cu-Csi-037
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM37
• Cu-Csi-038
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM38
• Cu-Csi-039
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM39
• Cu-Csi-040
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM40
• Cu-Csi-041
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM41
• Cu-Csi-042
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM42
• Cu-Csi-043
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM43
• Cu-Csi-044
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM44
• Cu-Csi-045
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM45
• Cy-Dar-001
  Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du 4ème degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de trois modèles représentent la même cyclide de Darboux avec deux familles de cercles différentes à chaque fois, ce qui fait bien six familles au total.
• Cy-Dar-002
  Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du 4ème degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de trois modèles représentent la même cyclide de Darboux avec deux familles de cercles différentes à chaque fois, ce qui fait bien six familles au total.
• Cy-Dar-003
  Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du 4ème degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de trois modèles représentent la même cyclide de Darboux avec deux familles de cercles différentes à chaque fois, ce qui fait bien six familles au total.
• Cy-Dar-004
  Système triplement orthogonal. Un système triplement orthogonal est formé de trois familles à un paramètre de surfaces, telles que chaque surface d'une famille coupe orthogonalement les surfaces des deux autres familles. Autrement dit, en chaque point de l'espace où trois surfaces se rencontrent, les trois plans tangents forment un trièdre trirectangle. Ce modèle est le système triple de Lamé, découvert par Gabriel Lamé en 1833. Il est constitué de quadriques homofocales. En chaque point se rencontrent orthogonalement un ellipsoïde, un hyperboloïde à une nappe et un hyperboloïde à deux nappes. L'un des intérêts des systèmes triplement orthogonaux tient au fait que deux familles du système découpent sur une surface de la troisième famille le réseau de ses lignes de courbure, autrement dit des courbes le long desquelles la courbure de la surface reste constamment maximale ou minimale.
• Cy-Dar-005
  Système triplement orthogonal. Un système triplement orthogonal est formé de trois familles à un paramètre de surfaces, telles que chaque surface d'une famille coupe orthogonalement les surfaces des deux autres familles. Autrement dit, en chaque point de l'espace où trois surfaces se rencontrent, les trois plans tangents forment un trièdre trirectangle. Ce modèle est le système triple de Serret, il illustre le système découvert par Joseph-Alfred Serret en 1847. Il est constitué d'une famille de paraboloïdes hyperboliques et de deux familles de surfaces du 4ème degré. L'un des intérêts des systèmes triplement orthogonaux tient au fait que deux familles du système découpent sur une surface de la troisième famille le réseau de ses lignes de courbure, autrement dit des courbes le long desquelles la courbure de la surface reste constamment maximale ou minimale.
• Cy-Dar-006
  Système triplement orthogonal. Un système triplement orthogonal est formé de trois familles à un paramètre de surfaces, telles que chaque surface d'une famille coupe orthogonalement les surfaces des deux autres familles. Autrement dit, en chaque point de l'espace où trois surfaces se rencontrent, les trois plans tangents forment un trièdre trirectangle. Ce modèle est le système triple de Darboux, il fait le lien avec ses recherches sur les cyclides. Il s'agit en effet du système triplement orthogonal de cyclides de Darboux tel qu'il est défini dans la thèse de Darboux. L'un des intérêts des systèmes triplement orthogonaux tient au fait que deux familles du système découpent sur une surface de la troisième famille le réseau de ses lignes de courbure, autrement dit des courbes le long desquelles la courbure de la surface reste constamment maximale ou minimale.
• Cy-Dup-020
  L'inversion de centre \( 0 \) et de rapport \( 1 \) est une transformation de l'espace qui échange tout point distinct de \( 0 \) avec un point de la même demi-droite issue de \( 0 \) et dont la distance à l'origine est l'inverse de celle du point de départ. Cette transformation jouit de la propriété de transformer les cercles en cercles, à condition toutefois de considérer les droites comme des cercles de rayon infini. Il en résulte que l'inverse d'un tore contient, comme le tore, quatre familles de cercles. Une telle surface s'appelle cyclide de Dupin. Elles ont été découvertes par Charles Dupin en 1822. Selon la position du centre d'inversion par rapport au tore, l'aspect de la cyclide varie. Pour ce modèle (cyclide parabolique), le centre d'inversion est sur le tore. Les cyclides de Dupin, comme les tores, sont des surfaces du 4ème degré.