-
 Portrait d'Émile Borel
Portrait d'Émile Borel Représentation d’Émile Borel dans son bureau à l’Institut Henri Poincaré.
Le peintre André Léveillé a notamment été le premier secrétaire général du Palais de la Découverte en 1935, puis son directeur de 1946 à 1960. Les deux hommes se connaissaient bien puisque Borel fut le 1er chef de la section de mathématiques du Palais.
-
 Hommage à Maurice Audin
Hommage à Maurice Audin Inscription :
"الجمهورية الجزائرية الديمقراطية الشعبية
وزارة التعليم العالي والبحث العلمي
En hommage à Maurice Audin
Alger le 10 décembre 2018"
-
 Prix Clay Mathematic Institute à G. Perelman
Prix Clay Mathematic Institute à G. Perelman Inscription recto :
"The Clay Mathematics Institute hereby awards the Millenium Prize for the resolution of the Poincaré conjecture to Grigory Perelman
June 8, 2010
The Poincaré conjecture:
If a smooth compact 3-manifold is simply connected, then it is homeomorphic to the 3-sphere."
-
 Buste de Jean Perrin
Buste de Jean Perrin Il existe plusieurs copies de ce buste réalisé par l’artiste Lydia Luzanovsky-Marinesco (1899-1983), élève du sculpteur Antoine Bourdelle (1861-1929). Originellement installé dans le Laboratoire de Chimie Physique, ce buste fut déplacé à l’Institut Henri Poincaré par Francis Perrin (1901-1992), lorsqu’il s’y installa en 1940.
-
 Buste d'Émile Borel
Buste d'Émile Borel
-
 Le promeneur de mathématiques
Le promeneur de mathématiques Oeuvre donnée par l’artiste à la bibliothèque suite à l’exposition « Promenade en mathématiques » en 2016.
-
 Coucher de soleil Vershik—Kerov—Logan—Shepp
Coucher de soleil Vershik—Kerov—Logan—Shepp Une interface aléatoire (diagramme de Young), séparant le rouge et le jaune et dépeignant une représentation Plancherel-aléatoire du groupe symétrique sur 2 304 lettres, approche la courbe « arctique » limite déterministe de Vershik—Kerov—Logan—Shepp. Ce qui est remarquable est que n’importe quelle interface Plancherel-aléatoire parmi les 3 x 1053 telles interfaces environ ressemblera, vue de loin, a celle-là en particulier. Ce résultat répond à une loi connue sous le nom de loi des grands nombres.
Donné à l'IHP par Dan Betea en 2017 dans le cadre du trimestre de recherche "Combinatorics and interactions" organisé par le Centre Émile Borel.
-
 Liquid #1
Liquid #1 Donné à l'IHP par Dan Betea en 2017 dans le cadre du trimestre de recherche "Combinatorics and interactions" organisé par le Centre Émile Borel.
-
 Tableau noir d'Émile Borel
Tableau noir d'Émile Borel Tableau exposé dès l'ouverture de la salle Pi du Palais de la découverte à Paris, en 1937.
Il s'agit d'une copie réalisée à partir d'une photo d'un tableau d'Emile Borel prise lors d'un de ses cours à l'université. Le support utilisé est un panneau de bois recouvert de peinture à tableau, sur laquelle la photo était reproduite à la peinture blanche.
À l'époque où l'éducation nationale usait de la craie, les enfants qui défilaient au Palais de la découverte avaient de la craie dans les poches et écrivaient sur le tableau de Borel. On pouvait effacer leurs bêtises sans effacer la peinture blanche reproduisant l'écriture de Borel.
-
 Maquette de la salle Pi
Maquette de la salle Pi Maquette à toucher échelle 1/30 de la salle Pi du Palais de la découverte, fondé en 1937 par Jean Perrin. Sa fonctionnalité était de permettre au public malvoyant présent physiquement dans la salle de se la représenter grâce au braille présent sur la maquette.
La salle Pi, dédiée aux mathématiques était présente dès 1937. On y trouvait les 707 premières décimales du célèbre nombre π (« pi ») telles que publiées en 1874 par William Shanks, qui avait passé 20 de sa vie à les calculer… à la main !
En 1946, Ferguson met en évidence une erreur : les décimales de Shanks sont fausses à partir de la 528ème. Les décimales de π seront corrigées plus tard, grâce au calcul par ordinateur. Aujourd’hui, on sait en calculer plusieurs milliers de milliards – et le record ne cesse d’être battu !
-
 Buste d'Henri Poincaré
Buste d'Henri Poincaré
-
 Cryptographe à réglettes
Cryptographe à réglettes Cryptographe à réglettes inventée par Arthur Hermann, construit d'après le système de Bazeries.
-
 Plateau de jeu #1
Plateau de jeu #1 Plateau de jeu inconnu.
-
 Plateau de jeu #2
Plateau de jeu #2 Plateau de jeu inconnu.
-
 Pavés Florentin du père Sébastien
Pavés Florentin du père Sébastien Jeu conçu par Édouard Lucas et édité par Chambon & Baye pour l'exposition universelle de 1889 à Paris. Le plateau composé de pavés mi-partis permet la diffusion d'un savoir mathématique lié aux combinaisons. Ces pavés sont des carrés du plan divisés par une diagonale en deux parties de couleur différente.
-
 Jeu d'empilement #2
Jeu d'empilement #2 Plateau de jeu d'empilement.
-
 Parcours du cavalier
Parcours du cavalier Problème : peut-on parcourir toutes les cases d'un échiquier en effectuant des sauts de cavalier ?
Dans ce montage dû à Édouard Lucas, les 64 cases sont matérialisées par les tiges, et le trajet du cavalier par les chaines brisées.
La solution présentée ici est due à Euler et fournit un trajet fermé.
-
 Jeu d'empilement #1
Jeu d'empilement #1 Plateau de jeu d'empilement.
-
 Timbre en hommage à Sophie Germain
Timbre en hommage à Sophie Germain Timbre hommage de la Collection Historique du Timbre-Poste Français, réalisé en marge de l'exposition "Sophie Germain : 1776 - 1831" exposée à l'IHP en 2016.
-
 Timbre commémoratif de l'ICM 1998 à Berlin
Timbre commémoratif de l'ICM 1998 à Berlin Timbre réalisé par la Deutsche Post AG à l'occasion de l'International Congress of Mathematicians de 1998 à Berlin.
Motif : décomposition d'un presque carré en carrés différents les uns des autres sur fond de nombre circulaire Pi.
-
 Ellipsoïde laqué
Ellipsoïde laqué Ellipsoïde réalisé par tranches successives de contreplaqué assemblées par Pierre Gallais (Lyon), puis couvert d'une laque végétale "urushi" par Martine Rey (Voiron).
-
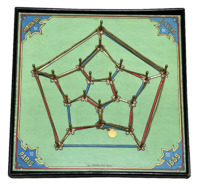 Jeu icosien de Hamilton
Jeu icosien de Hamilton Considérons les 20 sommets d'un dodécaèdre comme des villes et les 30 arêtes comme des routes.
Existe-t-il un trajet passant par chaque ville une fois et une seule et revenant au point de départ ?
Dans cette réalisation due à Édouard Lucas le dodécaèdre est figuré sous la forme d'une carte plane et la chainette matérialise un tel trajet.
-
 Photographie T. Chotteau #1
Photographie T. Chotteau #1 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP.
-
 Photographie T. Chotteau #2
Photographie T. Chotteau #2 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP.
-
 Photographie T. Chotteau #3
Photographie T. Chotteau #3 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP.
-
 Abstraction géométrique "Le Carré"
Abstraction géométrique "Le Carré" « Art du trait, rigueur de la forme, poésie des couleurs.
Carrément carré, les carrés dans le carré. Quel est le nombre de carrés dans ce carré ? Le nombre d'intersections ? Pour quel résultat selon la suite de Fibonacci ? »
Donné à l'IHP par Gine Delauney en 2016.
-
 Surface de Boy
Surface de Boy Peinture donnée par l'artiste à la bibliothèque suite à l'exposition "Patrice Jeener, le graveur de mathématiques", en 2016.
-
 Art conceptuel "Construction"
Art conceptuel "Construction" « J'ai fait cette toile en hommage à un être lumineux "un homme de savoir" qui s'implique dans la vie de la cité.
En écho à la pensée de Marcel Duchamp : "La peinture ne doit pas être exclusivement visuelle ou rétinienne. Elle doit aussi intéresser la matière grise, notre appétit de compréhension." »
Donné à l'IHP par Gine Delauney en 2016.
-
 Abstraction géométrique "La Joie"
Abstraction géométrique "La Joie" « Ma toile est joyeuse et dansante. Retenir que les belles choses de la vie et passent les nuages. »
Donné à l'IHP par Gine Delauney en 2016.
-
 Tableau D. Martet
Tableau D. Martet Oeuvre donnée par l’artiste à la bibliothèque suite à l’exposition « Promenade en mathématiques » en 2016.
-
 Photo de l'ICM 1954
Photo de l'ICM 1954 Photographie de tous les participants et participantes assemblés lors de l'ICM (International Congress of Mathematicians) de 1954 à Amsterdam.
-
 Abstraction géométrique "Équation"
Abstraction géométrique "Équation" « Beauté et équilibre en harmonie pour cette figure turquoise et soufre sur fond gris avec chiffres et lettres à la craie. J'aime faire des figures géométriques pour leur beauté, leur simplicité, pour les mystères qu'elles renferment et qu'elles nous cachent. »
Donné à l'IHP par Gine Delauney en 2016.
-
 Gravures centenaire Henri Poincaré
Gravures centenaire Henri Poincaré Gravures réalisées par Claude Gondard pour le centenaire de la disparition d'Henri Poincaré organisé par l'Institut Henri Poincaré et l'École polytechnique tout au long de l'année 2012.
L'institut conserve une gravure numérotée 45/350 et une épreuve numérotée IX/XXIV. Le dessin préparatoire numéroté 908 a été réalisé en 2010.
Ce dessin est aussi reporté sur une médaille commémorative réalisée par Claude Gondard et conservée à l'IHP.
-
 Tableau pliant du groupe Bourbaki
Tableau pliant du groupe Bourbaki Outil emblématique des mathématiques, le tableau noir favorise les échanges spontanés. Il permet d’écrire, de se tromper, d’effacer, de recommencer… à l’image du processus de recherche.
Les tableaux pliants permettaient au collectif de chercheurs Bourbaki de s’installer n’importe où pour travailler.
Ce tableau était conservé dans les archives de la bibliothèque de mathématiques et informatique du DMA de l'École normale supérieure. Il a été transféré à l'IHP en 2020.
-
 Chaire Jean Perrin
Chaire Jean Perrin
-
 Bureau de Jean Perrin
Bureau de Jean Perrin
 Portrait d'Émile Borel Représentation d’Émile Borel dans son bureau à l’Institut Henri Poincaré. Le peintre André Léveillé a notamment été le premier secrétaire général du Palais de la Découverte en 1935, puis son directeur de 1946 à 1960. Les deux hommes se connaissaient bien puisque Borel fut le 1er chef de la section de mathématiques du Palais.
Portrait d'Émile Borel Représentation d’Émile Borel dans son bureau à l’Institut Henri Poincaré. Le peintre André Léveillé a notamment été le premier secrétaire général du Palais de la Découverte en 1935, puis son directeur de 1946 à 1960. Les deux hommes se connaissaient bien puisque Borel fut le 1er chef de la section de mathématiques du Palais. Hommage à Maurice Audin Inscription : "الجمهورية الجزائرية الديمقراطية الشعبية وزارة التعليم العالي والبحث العلمي En hommage à Maurice Audin Alger le 10 décembre 2018"
Hommage à Maurice Audin Inscription : "الجمهورية الجزائرية الديمقراطية الشعبية وزارة التعليم العالي والبحث العلمي En hommage à Maurice Audin Alger le 10 décembre 2018" Prix Clay Mathematic Institute à G. Perelman Inscription recto : "The Clay Mathematics Institute hereby awards the Millenium Prize for the resolution of the Poincaré conjecture to Grigory Perelman June 8, 2010 The Poincaré conjecture: If a smooth compact 3-manifold is simply connected, then it is homeomorphic to the 3-sphere."
Prix Clay Mathematic Institute à G. Perelman Inscription recto : "The Clay Mathematics Institute hereby awards the Millenium Prize for the resolution of the Poincaré conjecture to Grigory Perelman June 8, 2010 The Poincaré conjecture: If a smooth compact 3-manifold is simply connected, then it is homeomorphic to the 3-sphere." Buste de Jean Perrin Il existe plusieurs copies de ce buste réalisé par l’artiste Lydia Luzanovsky-Marinesco (1899-1983), élève du sculpteur Antoine Bourdelle (1861-1929). Originellement installé dans le Laboratoire de Chimie Physique, ce buste fut déplacé à l’Institut Henri Poincaré par Francis Perrin (1901-1992), lorsqu’il s’y installa en 1940.
Buste de Jean Perrin Il existe plusieurs copies de ce buste réalisé par l’artiste Lydia Luzanovsky-Marinesco (1899-1983), élève du sculpteur Antoine Bourdelle (1861-1929). Originellement installé dans le Laboratoire de Chimie Physique, ce buste fut déplacé à l’Institut Henri Poincaré par Francis Perrin (1901-1992), lorsqu’il s’y installa en 1940. Buste d'Émile Borel
Buste d'Émile Borel
 Le promeneur de mathématiques Oeuvre donnée par l’artiste à la bibliothèque suite à l’exposition « Promenade en mathématiques » en 2016.
Le promeneur de mathématiques Oeuvre donnée par l’artiste à la bibliothèque suite à l’exposition « Promenade en mathématiques » en 2016. Coucher de soleil Vershik—Kerov—Logan—Shepp Une interface aléatoire (diagramme de Young), séparant le rouge et le jaune et dépeignant une représentation Plancherel-aléatoire du groupe symétrique sur 2 304 lettres, approche la courbe « arctique » limite déterministe de Vershik—Kerov—Logan—Shepp. Ce qui est remarquable est que n’importe quelle interface Plancherel-aléatoire parmi les 3 x 1053 telles interfaces environ ressemblera, vue de loin, a celle-là en particulier. Ce résultat répond à une loi connue sous le nom de loi des grands nombres. Donné à l'IHP par Dan Betea en 2017 dans le cadre du trimestre de recherche "Combinatorics and interactions" organisé par le Centre Émile Borel.
Coucher de soleil Vershik—Kerov—Logan—Shepp Une interface aléatoire (diagramme de Young), séparant le rouge et le jaune et dépeignant une représentation Plancherel-aléatoire du groupe symétrique sur 2 304 lettres, approche la courbe « arctique » limite déterministe de Vershik—Kerov—Logan—Shepp. Ce qui est remarquable est que n’importe quelle interface Plancherel-aléatoire parmi les 3 x 1053 telles interfaces environ ressemblera, vue de loin, a celle-là en particulier. Ce résultat répond à une loi connue sous le nom de loi des grands nombres. Donné à l'IHP par Dan Betea en 2017 dans le cadre du trimestre de recherche "Combinatorics and interactions" organisé par le Centre Émile Borel. Liquid #1 Donné à l'IHP par Dan Betea en 2017 dans le cadre du trimestre de recherche "Combinatorics and interactions" organisé par le Centre Émile Borel.
Liquid #1 Donné à l'IHP par Dan Betea en 2017 dans le cadre du trimestre de recherche "Combinatorics and interactions" organisé par le Centre Émile Borel. Tableau noir d'Émile Borel Tableau exposé dès l'ouverture de la salle Pi du Palais de la découverte à Paris, en 1937. Il s'agit d'une copie réalisée à partir d'une photo d'un tableau d'Emile Borel prise lors d'un de ses cours à l'université. Le support utilisé est un panneau de bois recouvert de peinture à tableau, sur laquelle la photo était reproduite à la peinture blanche. À l'époque où l'éducation nationale usait de la craie, les enfants qui défilaient au Palais de la découverte avaient de la craie dans les poches et écrivaient sur le tableau de Borel. On pouvait effacer leurs bêtises sans effacer la peinture blanche reproduisant l'écriture de Borel.
Tableau noir d'Émile Borel Tableau exposé dès l'ouverture de la salle Pi du Palais de la découverte à Paris, en 1937. Il s'agit d'une copie réalisée à partir d'une photo d'un tableau d'Emile Borel prise lors d'un de ses cours à l'université. Le support utilisé est un panneau de bois recouvert de peinture à tableau, sur laquelle la photo était reproduite à la peinture blanche. À l'époque où l'éducation nationale usait de la craie, les enfants qui défilaient au Palais de la découverte avaient de la craie dans les poches et écrivaient sur le tableau de Borel. On pouvait effacer leurs bêtises sans effacer la peinture blanche reproduisant l'écriture de Borel. Maquette de la salle Pi Maquette à toucher échelle 1/30 de la salle Pi du Palais de la découverte, fondé en 1937 par Jean Perrin. Sa fonctionnalité était de permettre au public malvoyant présent physiquement dans la salle de se la représenter grâce au braille présent sur la maquette. La salle Pi, dédiée aux mathématiques était présente dès 1937. On y trouvait les 707 premières décimales du célèbre nombre π (« pi ») telles que publiées en 1874 par William Shanks, qui avait passé 20 de sa vie à les calculer… à la main ! En 1946, Ferguson met en évidence une erreur : les décimales de Shanks sont fausses à partir de la 528ème. Les décimales de π seront corrigées plus tard, grâce au calcul par ordinateur. Aujourd’hui, on sait en calculer plusieurs milliers de milliards – et le record ne cesse d’être battu !
Maquette de la salle Pi Maquette à toucher échelle 1/30 de la salle Pi du Palais de la découverte, fondé en 1937 par Jean Perrin. Sa fonctionnalité était de permettre au public malvoyant présent physiquement dans la salle de se la représenter grâce au braille présent sur la maquette. La salle Pi, dédiée aux mathématiques était présente dès 1937. On y trouvait les 707 premières décimales du célèbre nombre π (« pi ») telles que publiées en 1874 par William Shanks, qui avait passé 20 de sa vie à les calculer… à la main ! En 1946, Ferguson met en évidence une erreur : les décimales de Shanks sont fausses à partir de la 528ème. Les décimales de π seront corrigées plus tard, grâce au calcul par ordinateur. Aujourd’hui, on sait en calculer plusieurs milliers de milliards – et le record ne cesse d’être battu ! Buste d'Henri Poincaré
Buste d'Henri Poincaré
 Cryptographe à réglettes Cryptographe à réglettes inventée par Arthur Hermann, construit d'après le système de Bazeries.
Cryptographe à réglettes Cryptographe à réglettes inventée par Arthur Hermann, construit d'après le système de Bazeries. Plateau de jeu #1 Plateau de jeu inconnu.
Plateau de jeu #1 Plateau de jeu inconnu. Plateau de jeu #2 Plateau de jeu inconnu.
Plateau de jeu #2 Plateau de jeu inconnu. Pavés Florentin du père Sébastien Jeu conçu par Édouard Lucas et édité par Chambon & Baye pour l'exposition universelle de 1889 à Paris. Le plateau composé de pavés mi-partis permet la diffusion d'un savoir mathématique lié aux combinaisons. Ces pavés sont des carrés du plan divisés par une diagonale en deux parties de couleur différente.
Pavés Florentin du père Sébastien Jeu conçu par Édouard Lucas et édité par Chambon & Baye pour l'exposition universelle de 1889 à Paris. Le plateau composé de pavés mi-partis permet la diffusion d'un savoir mathématique lié aux combinaisons. Ces pavés sont des carrés du plan divisés par une diagonale en deux parties de couleur différente. Jeu d'empilement #2 Plateau de jeu d'empilement.
Jeu d'empilement #2 Plateau de jeu d'empilement. Parcours du cavalier Problème : peut-on parcourir toutes les cases d'un échiquier en effectuant des sauts de cavalier ? Dans ce montage dû à Édouard Lucas, les 64 cases sont matérialisées par les tiges, et le trajet du cavalier par les chaines brisées. La solution présentée ici est due à Euler et fournit un trajet fermé.
Parcours du cavalier Problème : peut-on parcourir toutes les cases d'un échiquier en effectuant des sauts de cavalier ? Dans ce montage dû à Édouard Lucas, les 64 cases sont matérialisées par les tiges, et le trajet du cavalier par les chaines brisées. La solution présentée ici est due à Euler et fournit un trajet fermé. Jeu d'empilement #1 Plateau de jeu d'empilement.
Jeu d'empilement #1 Plateau de jeu d'empilement. Timbre en hommage à Sophie Germain Timbre hommage de la Collection Historique du Timbre-Poste Français, réalisé en marge de l'exposition "Sophie Germain : 1776 - 1831" exposée à l'IHP en 2016.
Timbre en hommage à Sophie Germain Timbre hommage de la Collection Historique du Timbre-Poste Français, réalisé en marge de l'exposition "Sophie Germain : 1776 - 1831" exposée à l'IHP en 2016. Timbre commémoratif de l'ICM 1998 à Berlin Timbre réalisé par la Deutsche Post AG à l'occasion de l'International Congress of Mathematicians de 1998 à Berlin. Motif : décomposition d'un presque carré en carrés différents les uns des autres sur fond de nombre circulaire Pi.
Timbre commémoratif de l'ICM 1998 à Berlin Timbre réalisé par la Deutsche Post AG à l'occasion de l'International Congress of Mathematicians de 1998 à Berlin. Motif : décomposition d'un presque carré en carrés différents les uns des autres sur fond de nombre circulaire Pi. Ellipsoïde laqué Ellipsoïde réalisé par tranches successives de contreplaqué assemblées par Pierre Gallais (Lyon), puis couvert d'une laque végétale "urushi" par Martine Rey (Voiron).
Ellipsoïde laqué Ellipsoïde réalisé par tranches successives de contreplaqué assemblées par Pierre Gallais (Lyon), puis couvert d'une laque végétale "urushi" par Martine Rey (Voiron). Jeu icosien de Hamilton Considérons les 20 sommets d'un dodécaèdre comme des villes et les 30 arêtes comme des routes. Existe-t-il un trajet passant par chaque ville une fois et une seule et revenant au point de départ ? Dans cette réalisation due à Édouard Lucas le dodécaèdre est figuré sous la forme d'une carte plane et la chainette matérialise un tel trajet.
Jeu icosien de Hamilton Considérons les 20 sommets d'un dodécaèdre comme des villes et les 30 arêtes comme des routes. Existe-t-il un trajet passant par chaque ville une fois et une seule et revenant au point de départ ? Dans cette réalisation due à Édouard Lucas le dodécaèdre est figuré sous la forme d'une carte plane et la chainette matérialise un tel trajet. Photographie T. Chotteau #1 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP.
Photographie T. Chotteau #1 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP. Photographie T. Chotteau #2 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP.
Photographie T. Chotteau #2 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP. Photographie T. Chotteau #3 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP.
Photographie T. Chotteau #3 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP. Abstraction géométrique "Le Carré" « Art du trait, rigueur de la forme, poésie des couleurs. Carrément carré, les carrés dans le carré. Quel est le nombre de carrés dans ce carré ? Le nombre d'intersections ? Pour quel résultat selon la suite de Fibonacci ? » Donné à l'IHP par Gine Delauney en 2016.
Abstraction géométrique "Le Carré" « Art du trait, rigueur de la forme, poésie des couleurs. Carrément carré, les carrés dans le carré. Quel est le nombre de carrés dans ce carré ? Le nombre d'intersections ? Pour quel résultat selon la suite de Fibonacci ? » Donné à l'IHP par Gine Delauney en 2016. Surface de Boy Peinture donnée par l'artiste à la bibliothèque suite à l'exposition "Patrice Jeener, le graveur de mathématiques", en 2016.
Surface de Boy Peinture donnée par l'artiste à la bibliothèque suite à l'exposition "Patrice Jeener, le graveur de mathématiques", en 2016. Art conceptuel "Construction" « J'ai fait cette toile en hommage à un être lumineux "un homme de savoir" qui s'implique dans la vie de la cité. En écho à la pensée de Marcel Duchamp : "La peinture ne doit pas être exclusivement visuelle ou rétinienne. Elle doit aussi intéresser la matière grise, notre appétit de compréhension." » Donné à l'IHP par Gine Delauney en 2016.
Art conceptuel "Construction" « J'ai fait cette toile en hommage à un être lumineux "un homme de savoir" qui s'implique dans la vie de la cité. En écho à la pensée de Marcel Duchamp : "La peinture ne doit pas être exclusivement visuelle ou rétinienne. Elle doit aussi intéresser la matière grise, notre appétit de compréhension." » Donné à l'IHP par Gine Delauney en 2016. Abstraction géométrique "La Joie" « Ma toile est joyeuse et dansante. Retenir que les belles choses de la vie et passent les nuages. » Donné à l'IHP par Gine Delauney en 2016.
Abstraction géométrique "La Joie" « Ma toile est joyeuse et dansante. Retenir que les belles choses de la vie et passent les nuages. » Donné à l'IHP par Gine Delauney en 2016. Tableau D. Martet Oeuvre donnée par l’artiste à la bibliothèque suite à l’exposition « Promenade en mathématiques » en 2016.
Tableau D. Martet Oeuvre donnée par l’artiste à la bibliothèque suite à l’exposition « Promenade en mathématiques » en 2016. Photo de l'ICM 1954 Photographie de tous les participants et participantes assemblés lors de l'ICM (International Congress of Mathematicians) de 1954 à Amsterdam.
Photo de l'ICM 1954 Photographie de tous les participants et participantes assemblés lors de l'ICM (International Congress of Mathematicians) de 1954 à Amsterdam. Abstraction géométrique "Équation" « Beauté et équilibre en harmonie pour cette figure turquoise et soufre sur fond gris avec chiffres et lettres à la craie. J'aime faire des figures géométriques pour leur beauté, leur simplicité, pour les mystères qu'elles renferment et qu'elles nous cachent. » Donné à l'IHP par Gine Delauney en 2016.
Abstraction géométrique "Équation" « Beauté et équilibre en harmonie pour cette figure turquoise et soufre sur fond gris avec chiffres et lettres à la craie. J'aime faire des figures géométriques pour leur beauté, leur simplicité, pour les mystères qu'elles renferment et qu'elles nous cachent. » Donné à l'IHP par Gine Delauney en 2016. Gravures centenaire Henri Poincaré Gravures réalisées par Claude Gondard pour le centenaire de la disparition d'Henri Poincaré organisé par l'Institut Henri Poincaré et l'École polytechnique tout au long de l'année 2012. L'institut conserve une gravure numérotée 45/350 et une épreuve numérotée IX/XXIV. Le dessin préparatoire numéroté 908 a été réalisé en 2010. Ce dessin est aussi reporté sur une médaille commémorative réalisée par Claude Gondard et conservée à l'IHP.
Gravures centenaire Henri Poincaré Gravures réalisées par Claude Gondard pour le centenaire de la disparition d'Henri Poincaré organisé par l'Institut Henri Poincaré et l'École polytechnique tout au long de l'année 2012. L'institut conserve une gravure numérotée 45/350 et une épreuve numérotée IX/XXIV. Le dessin préparatoire numéroté 908 a été réalisé en 2010. Ce dessin est aussi reporté sur une médaille commémorative réalisée par Claude Gondard et conservée à l'IHP. Tableau pliant du groupe Bourbaki Outil emblématique des mathématiques, le tableau noir favorise les échanges spontanés. Il permet d’écrire, de se tromper, d’effacer, de recommencer… à l’image du processus de recherche. Les tableaux pliants permettaient au collectif de chercheurs Bourbaki de s’installer n’importe où pour travailler. Ce tableau était conservé dans les archives de la bibliothèque de mathématiques et informatique du DMA de l'École normale supérieure. Il a été transféré à l'IHP en 2020.
Tableau pliant du groupe Bourbaki Outil emblématique des mathématiques, le tableau noir favorise les échanges spontanés. Il permet d’écrire, de se tromper, d’effacer, de recommencer… à l’image du processus de recherche. Les tableaux pliants permettaient au collectif de chercheurs Bourbaki de s’installer n’importe où pour travailler. Ce tableau était conservé dans les archives de la bibliothèque de mathématiques et informatique du DMA de l'École normale supérieure. Il a été transféré à l'IHP en 2020. Chaire Jean Perrin
Chaire Jean Perrin
 Bureau de Jean Perrin
Bureau de Jean Perrin