Collections de l'Institut Henri Poincaré Contenus
Identifiant contient
To-
-
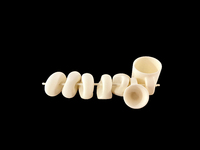To-001 Topology joke. "La blague traditionnelle sur les topologues est qu'ils ne peuvent pas faire la différence entre une tasse à café et un donut (ou si vous préférez, un beignet)." Surface obtenue en déformant continûment un tore : transformation de la tasse à la bouée. -
To-002 Topologie, le tore unilatère de Klein. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick. -
To-003 Topologie : analysis situs (étude de connexions). -
To-004 Topologie : tore coupé. -
To-005 Topologie : cylindres. -
To-006 Topologie : morceaux de sphères. -
To-007 Topologie : morceaux de sphères. -
To-008 Topologie : morceaux de sphères. -
To-009 Topologie : assemblages de parallélépipèdes. -
To-010 Topologie : morceaux de tores. -
To-011 Topologie : morceaux de tores. -
To-012 Topologie : tore. -
To-013 Topologie : morceaux de sphères. -
To-Sno-001 Cyclide unilatère. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick. -
To-Sno-002 Ruban de Möbius à bord circulaire. -
To-Sno-003 Bouteille de Klein en verre. -
To-Sno-004 Ruban de Möbius en bois. -
To-Sno-005 Sphère à bonnet croisé. Image du plan projectif avec 2 points pinces. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick. -
To-Sno-006 Bonnet croisé. Surface du 4ème ordre avec une droite double : lieu géométrique des cercles de courbure des sections normales d'une surface quelconque dans un élément de surface à courbure positive. -
To-Sno-007 La surface romaine de Steiner avec des courbes de tangente principale. Elle possède trois droites doubles qui se rejoignent en un point. -
To-Sno-008 Modèle de la représentation du plan projectif sur une surface sans singularité fermée dans le fini. Cette surface possède un minimum, un maximum et un maximum minimal et est ainsi la généralisation la plus simple de la sphère en ce qui concerne les extrêmes. -
To-Sno-009 Surface de Boy. Modèles de la représentation du plan projectif sur une surface fermée sans singularité. Cette surface possède un axe de symétrie, de sorte que la surface coïncide avec elle-même lors d'une rotation de 120° autour de celle-ci. -
To-Sno-010 Ruban de Möbius coupé en deux par le milieu formant deux rubans ordinaires enlacés. -
To-Sno-011 Ruban de Möbius avec alphabet. -
To-Sno-012 Ruban de Möbius. -
To-Sno-013 Il s'agit d'une surface du 4ème degré possédant deux singularités du type parapluie de Withney et une ligne double qui est la droite joignant les deux singularités. Cette surface (bonnet croisé) est une image du plan projectif réel avec auto-intersection. Dans son célèbre traité sur les surfaces, Darboux évoque l'impossibilité de représenter le plan projectif dans l'espace euclidien sans auto-intersection. Sa démonstration, quoique très instructive, est incomplète car elle s'appuie sur le fait que la surface cherchée est algébrique. -
To-Sno-014 Surface romaine de Steiner. -
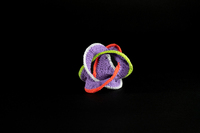To-Sno-015 Surface non orientable bordée par des anneaux borroméens. Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html). -
To-Sno-016 Ruban de Möbius (surface non orientable) bordé par un nœud de trèfle. -
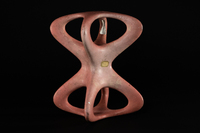To-Sor-001 Surface de genre 6. -
To-Sor-002 Tore carré plat plongé isométriquement dans l'espace ambiant. -
To-Sor-003 Carte sur la surface de genre 2 nécessitant 8 couleurs. -
To-Sor-004 Surface de Morin du huitième degré. -
To-Sor-005 Surface de genre 3 à symétrie d'ordre 4. -
To-Sor-006 On trace, dans un plan vertical, une droite verticale et un cercle non centré sur la droite, puis on fait tourner le plan autour de la droite prise comme axe de révolution. Le tore est la surface décrite par le cercle. Par construction le tore contient donc une famille de cercles appelés "méridiens". Lorsque l'on coupe le tore par des plans horizontaux, on trouve une autre famille de cercles appelés "parallèles". Il existe deux autres familles de cercles sur le tore, les "cercles d'Yvon Villarceau" nommés en hommage à leur découvreur, Antoine Yvon Villarceau. Ils sont obtenus en coupant le tore par un plan bitangent, autrement dit tangent au tore en exactement deux points distincts. On observe alors qu'un tel plan coupe le tore en deux parties égales. Inversement, est-ce qu'un plan qui coupe le tore en deux parties égales le coupe suivant deux cercles ? La réponse est non, comme le montre ce modèle-ci, sur lequel l'intersection est une courbe de 4ème degré, car le tore lui-même est une surface du 4ème degré. -
To-Sor-007 On trace, dans un plan vertical, une droite verticale et un cercle non centré sur la droite, puis on fait tourner le plan autour de la droite prise comme axe de révolution. Le tore est la surface décrite par le cercle. Par construction le tore contient donc une famille de cercles appelés "méridiens". Lorsque l'on coupe le tore par des plans horizontaux, on trouve une autre famille de cercles appelés "parallèles". Il existe deux autres familles de cercles sur le tore, les "cercles d'Yvon Villarceau" nommés en hommage à leur découvreur, Antoine Yvon Villarceau. Ils sont obtenus en coupant le tore par un plan bitangent, autrement dit tangent au tore en exactement deux points distincts, comme sur ce modèle-ci. On observe alors qu'un tel plan coupe le tore en deux parties égales. Inversement, est-ce qu'un plan qui coupe le tore en deux parties égales le coupe suivant deux cercles ? La réponse est non, l'intersection est alors une courbe de 4ème degré, car le tore lui-même est une surface du 4ème degré. -
To-Sor-008 Carte complète à 7 couleurs sur un tore. Réalisé d’après la technique du "bead crochet" (Ellie Baker and Susan Goldstine : Crafting Conundrums / CRC Press, 2014). -
To-Sor-009 Surface bordée par un entrelacs de trois anneaux. -
To-Sor-010 Surface de Seifert pour un entrelacs de Hopf (Seifert surface for a Hopf link). -
To-Sor-011 Surface de Seifert pour des anneaux borroméens. -
To-Sor-013 Surface de Seifert pour un nœud de trèfle "main gauche" (Seifert surface for a left-handed trefoil). Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html). -
To-Sor-014 Surface de Seifert pour un nœud de trèfle "main gauche" (Seifert surface for a left-handed trefoil). Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html). -
To-Sor-015 Surface orientable bordée par un nœud de Conway. -
To-Sor-016 Surface orientable bordée par un nœud à 5 croisements (5_2). -
To-Sor-017 Surface orientable de genre 1 bordée par un non-nœud. -
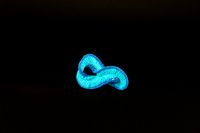To-Sor-018 Surface orientable bordée par un nœud de huit.