Contenus

Recherche avancée

Sg-001
Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc.
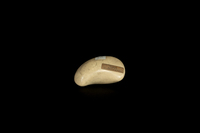Sg-002
Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc.
Sg-Lgc-001
Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé (celui-ci), un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux.
Sg-Lgc-002
Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux (celui-ci).
Sg-Lgc-003
Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie (celui-ci), le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux .
Sg-Sta-001
Gömböc 1928.
Sg-Sta-002
Gömböc en plexiglass.