Collections de l'Institut Henri Poincaré Contenus
Identifiant contient
To-Sno-
-
To-Sno-016 Ruban de Möbius (surface non orientable) bordé par un nœud de trèfle. -
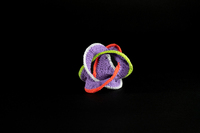To-Sno-015 Surface non orientable bordée par des anneaux borroméens. Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html). -
To-Sno-014 Surface romaine de Steiner. -
To-Sno-013 Il s'agit d'une surface du 4ème degré possédant deux singularités du type parapluie de Withney et une ligne double qui est la droite joignant les deux singularités. Cette surface (bonnet croisé) est une image du plan projectif réel avec auto-intersection. Dans son célèbre traité sur les surfaces, Darboux évoque l'impossibilité de représenter le plan projectif dans l'espace euclidien sans auto-intersection. Sa démonstration, quoique très instructive, est incomplète car elle s'appuie sur le fait que la surface cherchée est algébrique. -
To-Sno-012 Ruban de Möbius. -
To-Sno-011 Ruban de Möbius avec alphabet. -
To-Sno-010 Ruban de Möbius coupé en deux par le milieu formant deux rubans ordinaires enlacés. -
To-Sno-009 Surface de Boy. Modèles de la représentation du plan projectif sur une surface fermée sans singularité. Cette surface possède un axe de symétrie, de sorte que la surface coïncide avec elle-même lors d'une rotation de 120° autour de celle-ci. -
To-Sno-008 Modèle de la représentation du plan projectif sur une surface sans singularité fermée dans le fini. Cette surface possède un minimum, un maximum et un maximum minimal et est ainsi la généralisation la plus simple de la sphère en ce qui concerne les extrêmes. -
To-Sno-007 La surface romaine de Steiner avec des courbes de tangente principale. Elle possède trois droites doubles qui se rejoignent en un point. -
To-Sno-006 Bonnet croisé. Surface du 4ème ordre avec une droite double : lieu géométrique des cercles de courbure des sections normales d'une surface quelconque dans un élément de surface à courbure positive. -
To-Sno-005 Sphère à bonnet croisé. Image du plan projectif avec 2 points pinces. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick. -
To-Sno-004 Ruban de Möbius en bois. -
To-Sno-003 Bouteille de Klein en verre. -
To-Sno-002 Ruban de Möbius à bord circulaire. -
To-Sno-001 Cyclide unilatère. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.