Contenus

Recherche avancée

To-Sor-015
Surface orientable bordée par un nœud de Conway.
To-Sor-016
Surface orientable bordée par un nœud à 5 croisements (5_2).
To-Sor-013
Surface de Seifert pour un nœud de trèfle "main gauche" (Seifert surface for a left-handed trefoil). Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html).
To-Sor-017
Surface orientable de genre 1 bordée par un non-nœud.
To-Sor-003
Carte sur la surface de genre 2 nécessitant 8 couleurs.
To-Sor-009
Surface bordée par un entrelacs de trois anneaux.
To-Sor-011
Surface de Seifert pour des anneaux borroméens.
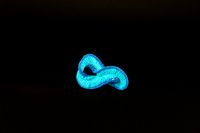To-Sor-018
Surface orientable bordée par un nœud de huit.
To-Sor-010
Surface de Seifert pour un entrelacs de Hopf (Seifert surface for a Hopf link).
To-Sor-014
Surface de Seifert pour un nœud de trèfle "main gauche" (Seifert surface for a left-handed trefoil). Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html).
To-Sor-002
Tore carré plat plongé isométriquement dans l'espace ambiant.
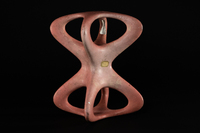To-Sor-001
Surface de genre 6.
To-Sor-005
Surface de genre 3 à symétrie d'ordre 4.
To-Sor-004
Surface de Morin du huitième degré.
To-Sor-008
Carte complète à 7 couleurs sur un tore. Réalisé d’après la technique du "bead crochet" (Ellie Baker and Susan Goldstine : Crafting Conundrums / CRC Press, 2014).
To-Sor-006
On trace, dans un plan vertical, une droite verticale et un cercle non centré sur la droite, puis on fait tourner le plan autour de la droite prise comme axe de révolution. Le tore est la surface décrite par le cercle. Par construction le tore contient donc une famille de cercles appelés "méridiens". Lorsque l'on coupe le tore par des plans horizontaux, on trouve une autre famille de cercles appelés "parallèles". Il existe deux autres familles de cercles sur le tore, les "cercles d'Yvon Villarceau" nommés en hommage à leur découvreur, Antoine Yvon Villarceau. Ils sont obtenus en coupant le tore par un plan bitangent, autrement dit tangent au tore en exactement deux points distincts. On observe alors qu'un tel plan coupe le tore en deux parties égales. Inversement, est-ce qu'un plan qui coupe le tore en deux parties égales le coupe suivant deux cercles ? La réponse est non, comme le montre ce modèle-ci, sur lequel l'intersection est une courbe de 4ème degré, car le tore lui-même est une surface du 4ème degré.
To-Sor-007
On trace, dans un plan vertical, une droite verticale et un cercle non centré sur la droite, puis on fait tourner le plan autour de la droite prise comme axe de révolution. Le tore est la surface décrite par le cercle. Par construction le tore contient donc une famille de cercles appelés "méridiens". Lorsque l'on coupe le tore par des plans horizontaux, on trouve une autre famille de cercles appelés "parallèles". Il existe deux autres familles de cercles sur le tore, les "cercles d'Yvon Villarceau" nommés en hommage à leur découvreur, Antoine Yvon Villarceau. Ils sont obtenus en coupant le tore par un plan bitangent, autrement dit tangent au tore en exactement deux points distincts, comme sur ce modèle-ci. On observe alors qu'un tel plan coupe le tore en deux parties égales. Inversement, est-ce qu'un plan qui coupe le tore en deux parties égales le coupe suivant deux cercles ? La réponse est non, l'intersection est alors une courbe de 4ème degré, car le tore lui-même est une surface du 4ème degré.