Collections de l'Institut Henri Poincaré

Contenus

• Cu-Csi-033
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM33
• Cu-Csi-039
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM39
• Cu-Csi-067
  Cubique (surface du 3ème degré) avec 1 point double biplanaire, 2 points doubles réels, et plans tangents réels.
• Cu-Csi-055
  Quelques exemples de surfaces du 3ème degré, aussi appelées cubiques. Ce sont des surfaces dont l’équation algébrique \(f(x,y,x)=0\) ne comporte que des termes dont le degré est inférieur ou égal à 3 (par exemple \(z^3+x^2y+xz+3=0\)) Il existe une très grande variété de formes, mais on a pu montrer, à la fin du siècle dernier, comment en faire une classification sommaire en fonction du nombre de droites réelles qui appartiennent à la surface : une cubique contient soit une infinité de droites réelles, et c’est alors une surface réglée, soit un nombre fini de droites réelles qui ne peut excéder 27. Par ailleurs, en faisant varier continûment les coefficients, on fait apparaitre ou disparaitre certaines de ces droites, ou certains points particuliers.
• Cu-Csi-050
  Quelques exemples de surfaces du 3ème degré, aussi appelées cubiques. Ce sont des surfaces dont l’équation algébrique \(f(x,y,x)=0\) ne comporte que des termes dont le degré est inférieur ou égal à 3 (par exemple \(z^3+x^2y+xz+3=0\)) Il existe une très grande variété de formes, mais on a pu montrer, à la fin du siècle dernier, comment en faire une classification sommaire en fonction du nombre de droites réelles qui appartiennent à la surface : une cubique contient soit une infinité de droites réelles, et c’est alors une surface réglée, soit un nombre fini de droites réelles qui ne peut excéder 27. Par ailleurs, en faisant varier continûment les coefficients, on fait apparaitre ou disparaitre certaines de ces droites, ou certains points particuliers.
• Cu-Csi-001
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM1
• Cu-Csi-002
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM2
• Cu-Csi-003
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM3
• Cu-Csi-004
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM4
• Cu-Csi-005
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM5
• Cu-Csi-006
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM6
• Cu-Csi-007
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM7
• Cu-Csi-008
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM8
• Cu-Csi-009
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM9
• Cu-Csi-010
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM10
• Cu-Csi-011
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM11
• Cu-Csi-012
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM12
• Cu-Csi-013
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM13
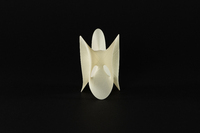• Cu-Csi-014
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM14
• Cu-Csi-015
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM15
• Cu-Csi-016
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM16
• Cu-Csi-017
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM17
• Cu-Csi-018
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM18
• Cu-Csi-019
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM19
• Cu-Csi-020
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM20
• Cu-Csi-021
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM21
• Cu-Csi-022
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM22
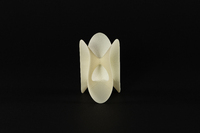• Cu-Csi-023
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM23
• Cu-Csi-024
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM24
• Cu-Csi-025
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM25
• Cu-Csi-026
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM26
• Cu-Csi-027
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM27
• Cu-Csi-028
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM28
• Cu-Csi-029
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM29
• Cu-Csi-030
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM30
• Cu-Csi-031
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM31
• Cu-Csi-032
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM32
• Cu-Csi-034
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM34
• Cu-Csi-035
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM35
• Cu-Csi-036
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM36
• Cu-Csi-037
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM37
• Cu-Csi-038
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM38
• Cu-Csi-040
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM40
• Cu-Csi-041
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM41
• Cu-Csi-042
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM42
• Cu-Csi-043
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM43
• Cu-Csi-044
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM44
• Cu-Csi-045
  Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM45
• Cu-Csi-051
  Quelques exemples de surfaces du 3ème degré, aussi appelées cubiques. Ce sont des surfaces dont l’équation algébrique \(f(x,y,x)=0\) ne comporte que des termes dont le degré est inférieur ou égal à 3 (par exemple \(z^3+x^2y+xz+3=0\)) Il existe une très grande variété de formes, mais on a pu montrer, à la fin du siècle dernier, comment en faire une classification sommaire en fonction du nombre de droites réelles qui appartiennent à la surface : une cubique contient soit une infinité de droites réelles, et c’est alors une surface réglée, soit un nombre fini de droites réelles qui ne peut excéder 27. Par ailleurs, en faisant varier continûment les coefficients, on fait apparaitre ou disparaitre certaines de ces droites, ou certains points particuliers.
• Cu-Csi-070
  Cubique (surface du 3ème degré) avec 4 points doubles réels. Le modèle est une forme affine du modèle numéro 45 (VII, 2).
• Cu-Csi-063
  Cubique (surface du 3ème degré) avec 4 points doubles réels.
• Cu-Csi-062
  Cubique (surface du 3ème degré) avec 4 points doubles réels. Le modèle est une forme affine du modèle numéro 45 (VII, 2).