-
 Gd-009
Gd-009 Surface définie paramétriquement.
-
 Gd-010
Gd-010 Surface correspondant à la sphère avec orthogonalité des éléments.
-
 Gd-011
Gd-011 Modèle de l'emplacement des centres des cordes d'une courbe gauche.
-
 Gd-012
Gd-012 Modèle de l'interface du réseau parabolique de rayons.
-
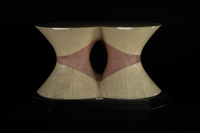 Gd-013
Gd-013 Hyperboloϊde double.
-
 Gd-014
Gd-014 Modèle de la surface \( z=x\ y\ \cdot \frac{x^2-y^2}{x^2+y^2} \), pour son point zéro singulier \( \frac{\delta^2\ z}{\delta\ x\ \delta\ y}\neq \frac{\delta^2\ z}{\delta\ y\ \delta\ x} \).
-
 Gd-015
Gd-015 Modèle d'une surface du 3ème degré, pour expliquer le comportement d'une surface courbe à proximité d'un point parabolique.
-
 Gd-016
Gd-016 Cône sinusoïdale à trois saillies et creux, avec sections horizontales. Cette surface est engendrée par une droite qui glisse sur une courbe sinusoïdale enroulée sur un cylindre et qui passe constamment par un même point situé sur l’axe de ce cylindre.
-
 Gd-017
Gd-017 Surface engendrée par une section plane d'un cylindre qui roule sur un cylindre.
-
 Gd-018
Gd-018 Graphe de la fonction \(z=\frac{x^2y^2}{(x^2+y^2)^{3/2}}\).
-
 Gd-App-001
Gd-App-001 Surface hélicoidale applicable sur l'éllipsoide de révolution, version en bois.
-
 Gd-App-002
Gd-App-002 Surface hélicoidale applicable sur l'éllipsoide de révolution.
-
 Gd-App-003
Gd-App-003 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b).
-
 Gd-App-004
Gd-App-004 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b), version en bois.
-
 Gd-App-005
Gd-App-005 Ellipsoïde de révolution, version en laiton flexible qui s'applique sur le modèle numéro 235 (VIII, 7c).
-
 Gd-App-006
Gd-App-006 Modèle d'une surface développable sur le paraboloïde de révolution de 12ème ordre et 10ème classe.
-
 Gd-App-007
Gd-App-007 Surface applicable sur le paraboloïde de révolution.
-
 Gd-App-008
Gd-App-008 Surface sur laquelle l'ellipsoïde est représenté de manière conforme par des normales parallèles.
-
 Gd-Can-001
Gd-Can-001 Surface canal hélicoϊdale et lignes de courbure.
-
 Gd-Can-002
Gd-Can-002 Surface spirale développée de sphère.
-
 Gd-Can-003
Gd-Can-003 Surface spirale lieu de cercles.
-
 Gd-Can-004
Gd-Can-004 Surface canal engendrée par une sphère de rayon constant.
-
 Gd-Cau-001
Gd-Cau-001 Surface du 12ème degré. Surface caustique des rayons partant d'une ligne lumineuse après leur réflexion sur un cylindre dont l'axe touche la ligne.
-
 Gd-Cau-002
Gd-Cau-002 Enveloppe de normales d'un conoïde de Plϋcker.
-
 Gd-Cau-003
Gd-Cau-003 Enveloppe de normales d'un paraboloïde.
-
 Gd-Cau-004
Gd-Cau-004 Enveloppe de normales d'un hyperboloïde.
-
 Gd-Cau-005
Gd-Cau-005 Enveloppe de normales d'un ellipsoïde.
-
 Gd-Cau-006
Gd-Cau-006 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires.
\(a=16, b=10, c=0\)
\(K=-1\)
-
 Gd-Cau-007
Gd-Cau-007 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires.
\(a=16, b=10, c=0\)
\(K=3\)
-
 Gd-Cau-008
Gd-Cau-008 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires.
\(a=16, b=10, c=0\)
\(K=\frac{b}{3}=\frac{10}{3}\)
-
 Gd-Cau-009
Gd-Cau-009 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires.
\(a=16, b=10, c=0\)
\(K=5,4\)
-
 Gd-Cau-010
Gd-Cau-010 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires.
\(a=16, b=10, c=0\)
\(K=8\)
-
 Gd-Cau-011
Gd-Cau-011 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires.
\(a=16, b=10, c=0\)
\(K=\frac{c}{3}=0\)
-
 Gd-Cau-012
Gd-Cau-012 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique.
Les deux enveloppes de la surface sont séparées, voir modèle n°118 I, 2a.
-
 Gd-Cau-013
Gd-Cau-013 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique.
Les deux enveloppes de la surface sont séparées, voir modèle n°119 I, 2a.
-
 Gd-Cau-014
Gd-Cau-014 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique.
Les deux enveloppes de la surface réunies (voir modèles n°118 et 119 I, 2a).
-
 Gd-Cau-015
Gd-Cau-015 Enveloppe des normales de l'hyperboloïde à une feuille.
Les deux enveloppes de la surface sont séparées, voir modèle n°122 I, 3a.
-
 Gd-Cau-016
Gd-Cau-016 Enveloppe des normales de l'hyperboloïde à une feuille.
Les deux enveloppes de la surface sont séparées, voir modèle n°121 I, 3a.
-
 Gd-Cau-017
Gd-Cau-017 Enveloppe des normales de l'hyperboloïde à une feuille.
Les deux manteaux réunis.
-
 Gd-Cau-018
Gd-Cau-018 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques."
La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires."
Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées.
-
 Gd-Cau-019
Gd-Cau-019 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques."
La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires."
Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées.
-
 Gd-Cau-020
Gd-Cau-020 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques."
La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires."
Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées.
-
 Gd-Cau-021
Gd-Cau-021 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques."
La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires."
Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées.
-
 Gd-Cau-022
Gd-Cau-022 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques."
La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires."
Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées.
-
 Gd-Cau-023
Gd-Cau-023 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques."
La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires."
Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées.
-
 Gd-Cau-024
Gd-Cau-024 Enveloppe des normales au paraboloïde.
\(y^2-z^1=2px\)
-
 Gd-Dev-001
Gd-Dev-001 Hélicoïde développable. Pour \( \varepsilon = \sigma \) ; la section normale à l'axe est une développante commune de cercle.
-
 Gd-Dev-002
Gd-Dev-002 Hélicoïde développable. Pour \( \varepsilon = \sigma \) ; la section normale à l'axe est une développante commune de cercle.
Version en carton du modèle n°127 (XX, 1a).
-
 Gd-Reg-001
Gd-Reg-001 Helicoïde développable.
-
 Gd-Reg-002
Gd-Reg-002 Surface hélicoïdale fermée droite, dans laquelle les génératrices rencontrent l'axe de l'hélice perpendiculairement.
-
 Gd-Reg-004
Gd-Reg-004 Surface réglée : deux conoïdes à base ellipsoïde.
Modèle inspiré de ceux réalisés dans les années 1830 par Théodore Olivier, géomètre professeur à l'École Centrale des Arts et Manufactures. Ses modèles furent fabriqués par deux constructeurs parisiens successifs : d'abord par l'entreprise "Pixii Père et Fils" (Hippolyte Pixii), qui devint "Fabre de Lagrange" dans les années 1870.
-
 Gd-Reg-005
Gd-Reg-005 Hyperboloïde à une feuille et son cône asymptote.
Modèle inspiré de ceux réalisés dans les années 1830 par Théodore Olivier, géomètre professeur à l'École Centrale des Arts et Manufactures. Ses modèles furent fabriqués par deux constructeurs parisiens successifs : d'abord par l'entreprise "Pixii Père et Fils" (Hippolyte Pixii), qui devint "Fabre de Lagrange" dans les années 1870.
 Gd-009 Surface définie paramétriquement.
Gd-009 Surface définie paramétriquement. Gd-010 Surface correspondant à la sphère avec orthogonalité des éléments.
Gd-010 Surface correspondant à la sphère avec orthogonalité des éléments. Gd-011 Modèle de l'emplacement des centres des cordes d'une courbe gauche.
Gd-011 Modèle de l'emplacement des centres des cordes d'une courbe gauche. Gd-012 Modèle de l'interface du réseau parabolique de rayons.
Gd-012 Modèle de l'interface du réseau parabolique de rayons. Gd-013 Hyperboloϊde double.
Gd-013 Hyperboloϊde double. Gd-014 Modèle de la surface \( z=x\ y\ \cdot \frac{x^2-y^2}{x^2+y^2} \), pour son point zéro singulier \( \frac{\delta^2\ z}{\delta\ x\ \delta\ y}\neq \frac{\delta^2\ z}{\delta\ y\ \delta\ x} \).
Gd-014 Modèle de la surface \( z=x\ y\ \cdot \frac{x^2-y^2}{x^2+y^2} \), pour son point zéro singulier \( \frac{\delta^2\ z}{\delta\ x\ \delta\ y}\neq \frac{\delta^2\ z}{\delta\ y\ \delta\ x} \). Gd-015 Modèle d'une surface du 3ème degré, pour expliquer le comportement d'une surface courbe à proximité d'un point parabolique.
Gd-015 Modèle d'une surface du 3ème degré, pour expliquer le comportement d'une surface courbe à proximité d'un point parabolique. Gd-016 Cône sinusoïdale à trois saillies et creux, avec sections horizontales. Cette surface est engendrée par une droite qui glisse sur une courbe sinusoïdale enroulée sur un cylindre et qui passe constamment par un même point situé sur l’axe de ce cylindre.
Gd-016 Cône sinusoïdale à trois saillies et creux, avec sections horizontales. Cette surface est engendrée par une droite qui glisse sur une courbe sinusoïdale enroulée sur un cylindre et qui passe constamment par un même point situé sur l’axe de ce cylindre. Gd-017 Surface engendrée par une section plane d'un cylindre qui roule sur un cylindre.
Gd-017 Surface engendrée par une section plane d'un cylindre qui roule sur un cylindre. Gd-018 Graphe de la fonction \(z=\frac{x^2y^2}{(x^2+y^2)^{3/2}}\).
Gd-018 Graphe de la fonction \(z=\frac{x^2y^2}{(x^2+y^2)^{3/2}}\). Gd-App-001 Surface hélicoidale applicable sur l'éllipsoide de révolution, version en bois.
Gd-App-001 Surface hélicoidale applicable sur l'éllipsoide de révolution, version en bois. Gd-App-002 Surface hélicoidale applicable sur l'éllipsoide de révolution.
Gd-App-002 Surface hélicoidale applicable sur l'éllipsoide de révolution. Gd-App-003 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b).
Gd-App-003 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b). Gd-App-004 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b), version en bois.
Gd-App-004 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b), version en bois. Gd-App-005 Ellipsoïde de révolution, version en laiton flexible qui s'applique sur le modèle numéro 235 (VIII, 7c).
Gd-App-005 Ellipsoïde de révolution, version en laiton flexible qui s'applique sur le modèle numéro 235 (VIII, 7c). Gd-App-006 Modèle d'une surface développable sur le paraboloïde de révolution de 12ème ordre et 10ème classe.
Gd-App-006 Modèle d'une surface développable sur le paraboloïde de révolution de 12ème ordre et 10ème classe. Gd-App-007 Surface applicable sur le paraboloïde de révolution.
Gd-App-007 Surface applicable sur le paraboloïde de révolution. Gd-App-008 Surface sur laquelle l'ellipsoïde est représenté de manière conforme par des normales parallèles.
Gd-App-008 Surface sur laquelle l'ellipsoïde est représenté de manière conforme par des normales parallèles. Gd-Can-001 Surface canal hélicoϊdale et lignes de courbure.
Gd-Can-001 Surface canal hélicoϊdale et lignes de courbure. Gd-Can-002 Surface spirale développée de sphère.
Gd-Can-002 Surface spirale développée de sphère. Gd-Can-003 Surface spirale lieu de cercles.
Gd-Can-003 Surface spirale lieu de cercles. Gd-Can-004 Surface canal engendrée par une sphère de rayon constant.
Gd-Can-004 Surface canal engendrée par une sphère de rayon constant. Gd-Cau-001 Surface du 12ème degré. Surface caustique des rayons partant d'une ligne lumineuse après leur réflexion sur un cylindre dont l'axe touche la ligne.
Gd-Cau-001 Surface du 12ème degré. Surface caustique des rayons partant d'une ligne lumineuse après leur réflexion sur un cylindre dont l'axe touche la ligne. Gd-Cau-002 Enveloppe de normales d'un conoïde de Plϋcker.
Gd-Cau-002 Enveloppe de normales d'un conoïde de Plϋcker. Gd-Cau-003 Enveloppe de normales d'un paraboloïde.
Gd-Cau-003 Enveloppe de normales d'un paraboloïde. Gd-Cau-004 Enveloppe de normales d'un hyperboloïde.
Gd-Cau-004 Enveloppe de normales d'un hyperboloïde. Gd-Cau-005 Enveloppe de normales d'un ellipsoïde.
Gd-Cau-005 Enveloppe de normales d'un ellipsoïde. Gd-Cau-006 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=-1\)
Gd-Cau-006 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=-1\) Gd-Cau-007 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=3\)
Gd-Cau-007 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=3\) Gd-Cau-008 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=\frac{b}{3}=\frac{10}{3}\)
Gd-Cau-008 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=\frac{b}{3}=\frac{10}{3}\) Gd-Cau-009 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=5,4\)
Gd-Cau-009 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=5,4\) Gd-Cau-010 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=8\)
Gd-Cau-010 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=8\) Gd-Cau-011 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=\frac{c}{3}=0\)
Gd-Cau-011 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=\frac{c}{3}=0\) Gd-Cau-012 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique. Les deux enveloppes de la surface sont séparées, voir modèle n°118 I, 2a.
Gd-Cau-012 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique. Les deux enveloppes de la surface sont séparées, voir modèle n°118 I, 2a. Gd-Cau-013 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique. Les deux enveloppes de la surface sont séparées, voir modèle n°119 I, 2a.
Gd-Cau-013 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique. Les deux enveloppes de la surface sont séparées, voir modèle n°119 I, 2a. Gd-Cau-014 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique. Les deux enveloppes de la surface réunies (voir modèles n°118 et 119 I, 2a).
Gd-Cau-014 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique. Les deux enveloppes de la surface réunies (voir modèles n°118 et 119 I, 2a). Gd-Cau-015 Enveloppe des normales de l'hyperboloïde à une feuille. Les deux enveloppes de la surface sont séparées, voir modèle n°122 I, 3a.
Gd-Cau-015 Enveloppe des normales de l'hyperboloïde à une feuille. Les deux enveloppes de la surface sont séparées, voir modèle n°122 I, 3a. Gd-Cau-016 Enveloppe des normales de l'hyperboloïde à une feuille. Les deux enveloppes de la surface sont séparées, voir modèle n°121 I, 3a.
Gd-Cau-016 Enveloppe des normales de l'hyperboloïde à une feuille. Les deux enveloppes de la surface sont séparées, voir modèle n°121 I, 3a. Gd-Cau-017 Enveloppe des normales de l'hyperboloïde à une feuille. Les deux manteaux réunis.
Gd-Cau-017 Enveloppe des normales de l'hyperboloïde à une feuille. Les deux manteaux réunis. Gd-Cau-018 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques." La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires." Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées.
Gd-Cau-018 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques." La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires." Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées. Gd-Cau-019 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques." La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires." Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées.
Gd-Cau-019 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques." La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires." Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées. Gd-Cau-020 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques." La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires." Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées.
Gd-Cau-020 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques." La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires." Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées. Gd-Cau-021 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques." La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires." Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées.
Gd-Cau-021 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques." La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires." Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées. Gd-Cau-022 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques." La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires." Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées.
Gd-Cau-022 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques." La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires." Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées. Gd-Cau-023 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques." La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires." Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées.
Gd-Cau-023 Ce modèle fait partie d'une série de six objets représentants les fronts d'ondes de Darboux. Il s'agit des reproductions de modèles en bois exécutés par Joseph Caron en 1914 (actuellement exposés dans la Maison Poincaré). Ce sont les solutions d'un problème résolu par Darboux en 1881 dans un article portant sur la notion de front d'onde, autrement dit sur les surfaces parallèles à une surface donnée. Darboux y énonce le théorème suivant : "Si une droit se meut de telle manière que trois de ses points soient toujours situés dans trois plans rectangulaires, elle demeurera, dans toutes ses positions, normale à une surface fixe, qui sera algébrique et de quatrième classe et dont les lignes de courbure seront aussi algébriques." La définition des modèles est données par Caron sous forme d'exercice : "Surface normale aux droites dont trois points de distances constantes se meuvent dans trois plans rectangulaires." Les modèles exécutés par Caron sont choisis de telle sorte qu'entre deux modèles consécutifs il y ait une transition générique appelée aujourd'hui "métamorphose", et que toutes les métamorphoses du front d'onde étudié soient balayées. Gd-Cau-024 Enveloppe des normales au paraboloïde. \(y^2-z^1=2px\)
Gd-Cau-024 Enveloppe des normales au paraboloïde. \(y^2-z^1=2px\) Gd-Dev-001 Hélicoïde développable. Pour \( \varepsilon = \sigma \) ; la section normale à l'axe est une développante commune de cercle.
Gd-Dev-001 Hélicoïde développable. Pour \( \varepsilon = \sigma \) ; la section normale à l'axe est une développante commune de cercle. Gd-Dev-002 Hélicoïde développable. Pour \( \varepsilon = \sigma \) ; la section normale à l'axe est une développante commune de cercle. Version en carton du modèle n°127 (XX, 1a).
Gd-Dev-002 Hélicoïde développable. Pour \( \varepsilon = \sigma \) ; la section normale à l'axe est une développante commune de cercle. Version en carton du modèle n°127 (XX, 1a). Gd-Reg-001 Helicoïde développable.
Gd-Reg-001 Helicoïde développable. Gd-Reg-002 Surface hélicoïdale fermée droite, dans laquelle les génératrices rencontrent l'axe de l'hélice perpendiculairement.
Gd-Reg-002 Surface hélicoïdale fermée droite, dans laquelle les génératrices rencontrent l'axe de l'hélice perpendiculairement. Gd-Reg-004 Surface réglée : deux conoïdes à base ellipsoïde. Modèle inspiré de ceux réalisés dans les années 1830 par Théodore Olivier, géomètre professeur à l'École Centrale des Arts et Manufactures. Ses modèles furent fabriqués par deux constructeurs parisiens successifs : d'abord par l'entreprise "Pixii Père et Fils" (Hippolyte Pixii), qui devint "Fabre de Lagrange" dans les années 1870.
Gd-Reg-004 Surface réglée : deux conoïdes à base ellipsoïde. Modèle inspiré de ceux réalisés dans les années 1830 par Théodore Olivier, géomètre professeur à l'École Centrale des Arts et Manufactures. Ses modèles furent fabriqués par deux constructeurs parisiens successifs : d'abord par l'entreprise "Pixii Père et Fils" (Hippolyte Pixii), qui devint "Fabre de Lagrange" dans les années 1870. Gd-Reg-005 Hyperboloïde à une feuille et son cône asymptote. Modèle inspiré de ceux réalisés dans les années 1830 par Théodore Olivier, géomètre professeur à l'École Centrale des Arts et Manufactures. Ses modèles furent fabriqués par deux constructeurs parisiens successifs : d'abord par l'entreprise "Pixii Père et Fils" (Hippolyte Pixii), qui devint "Fabre de Lagrange" dans les années 1870.
Gd-Reg-005 Hyperboloïde à une feuille et son cône asymptote. Modèle inspiré de ceux réalisés dans les années 1830 par Théodore Olivier, géomètre professeur à l'École Centrale des Arts et Manufactures. Ses modèles furent fabriqués par deux constructeurs parisiens successifs : d'abord par l'entreprise "Pixii Père et Fils" (Hippolyte Pixii), qui devint "Fabre de Lagrange" dans les années 1870.