-
 Ct-Neg-014
Ct-Neg-014 Surface de révolution à courbure totale constante négative (type hyperboloïde) version en bois sans lignes géodésiques parallèles et cercles géodésiques.
-
 Ct-Neg-015
Ct-Neg-015 Plan hyperbolique symétrique crocheté.
Donné par Daina Taimina suite à sa visite de la bibliothèque en 2011.
-
 Ct-Neg-016
Ct-Neg-016 Hélicoïde.
-
 Ct-Neg-017
Ct-Neg-017 Deux surfaces de révolution à courbure totale constante négative en tôle de laiton flexible, à l'aide desquelles on peut expliquer le pliage d'une telle surface sur une autre et son déplacement dessus, et plus généralement la notion de "géométrie" sur ces surfaces.
S'appliquent sur les modèles numéros 229 (II, 5), 231 (V, 4) et 232 (VIII, 1).
Les modèles numéros 229 (II, 5), 231 (V, 4) et 232 (VIII, 1) ont la même courbure. Pour montrer la possibilité de les dérouler l'un sur l'autre et surtout de les déplacer sur eux-mêmes, ainsi que pour montrer les étranges relations entre la géométrie non euclidienne et la géométrie de Lobatschewsky, on les a ajusté sur ces deux bandes de laiton mince. Si l'on découpe dans l'une d'entre elles un morceau triangulaire dont les côtés sont des lignes géodésiques (par exemple celles de la surface 229 (II, 5)), l'observation visuelle nous apprend déjà que la somme des angles dans un tel triangle est inférieure à \(2R\).
-
 Ct-Pos-001
Ct-Pos-001 Surface de révolution de courbure constante positive avec lignes géodésiques. Application sur la sphère, la méridienne ne rencontrant pas l'axe.
-
 Ct-Pos-002
Ct-Pos-002 Surface hélicoïdale de courbure constante positive.
-
 Ct-Pos-003
Ct-Pos-003 Surface de révolution de courbure constante positive, version en bois sans lignes géodésiques. Application sur la sphère, la méridienne rencontre l'axe.
-
 Ct-Pos-004
Ct-Pos-004 Surface de révolution de courbure constante positive avec lignes géodésiques. Application sur la sphère, la méridienne rencontre l'axe.
-
 Ct-Pos-005
Ct-Pos-005 Surface hélicoïdale de courbure constante positive.
-
 Ct-Pos-006
Ct-Pos-006 Surface de révolution de courbure constante positive avec lignes géodésiques. Application sur la sphère, la méridienne ne rencontrant pas l'axe.
-
 Ct-Pos-007
Ct-Pos-007 Demi-sphère creuse en tôle de laiton.
Les surfaces à courbure constante, conçues comme une fine peau, peuvent coulisser sur elles-mêmes et se dérouler les unes sur les autres. On peut en faire l'expérience avec les bandes de laiton souples suivantes, ajustées sur ces surfaces.
S'applique sur les modèles numéros 220 et 221 (V, 2a et b).
-
 Ct-Pos-009
Ct-Pos-009 Bande de surface à courbure positive constante en tôle de laiton. Zone sphérique correspondant à un angle centrifuge de presque 90°.
Les surfaces à courbure constante, conçues comme une fine peau, peuvent coulisser sur elles-mêmes et se dérouler les unes sur les autres. On peut en faire l'expérience avec les bandes de laiton souples suivantes, ajustées sur ces surfaces.
S'applique sur le modèle numéro 222 (V, 2c).
-
 Ct-Reg-001
Ct-Reg-001 Hélicoϊde engendré par le développement d'une hélice.
-
 Cu-001
Cu-001 Le pentaèdre de Sylvester de la surface diagonale de Clebsch.
-
 Cu-002
Cu-002 Surface hessienne du modèle numéro 50 (VII, 7).
-
 Cu-003
Cu-003 Partie étoilée du modèle numéro 64 (VII, 24a) pour un pentaèdre composé du plan infiniment éloigné et d'un tétraèdre régulier.
-
 Cu-Cne-001
Cu-Cne-001 Cône de genre un (de sixième classe), constitué d'une seule enveloppe non appariée en position carrée.
-
 Cu-Cne-002
Cu-Cne-002 Cône de genre zéro à double arête (de quatrième classe), qui se présente comme une double arête isolée.
-
 Cu-Cne-003
Cu-Cne-003 Cône de genre un (de sixième classe), constitué d'une seule enveloppe non appariée avec trois plans de retournement passant par une droite.
-
 Cu-Cne-004
Cu-Cne-004 Cône de genre zéro avec arête de retour (de troisième classe).
-
 Cu-Cne-005
Cu-Cne-005 Cône de genre un (de sixième classe), constitué d'une enveloppe appariée et d'une enveloppe non appariée.
-
 Cu-Cne-006
Cu-Cne-006 Cône de genre zéro à double arête (de quatrième classe), avec auto-intersection.
-
 Cu-Cne-007
Cu-Cne-007 Cône de genre un (de sixième classe), constitué d'une seule enveloppe non appariée en position triangulaire.
-
 Cu-Csi-001
Cu-Csi-001 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM1
-
 Cu-Csi-002
Cu-Csi-002 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM2
-
 Cu-Csi-003
Cu-Csi-003 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM3
-
 Cu-Csi-004
Cu-Csi-004 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM4
-
 Cu-Csi-005
Cu-Csi-005 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM5
-
 Cu-Csi-006
Cu-Csi-006 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM6
-
 Cu-Csi-007
Cu-Csi-007 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM7
-
 Cu-Csi-008
Cu-Csi-008 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM8
-
 Cu-Csi-009
Cu-Csi-009 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM9
-
 Cu-Csi-010
Cu-Csi-010 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM10
-
 Cu-Csi-011
Cu-Csi-011 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM11
-
 Cu-Csi-012
Cu-Csi-012 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM12
-
 Cu-Csi-013
Cu-Csi-013 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM13
-
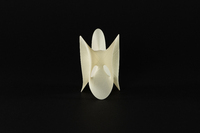 Cu-Csi-014
Cu-Csi-014 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM14
-
 Cu-Csi-015
Cu-Csi-015 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM15
-
 Cu-Csi-016
Cu-Csi-016 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM16
-
 Cu-Csi-017
Cu-Csi-017 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM17
-
 Cu-Csi-018
Cu-Csi-018 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM18
-
 Cu-Csi-019
Cu-Csi-019 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM19
-
 Cu-Csi-020
Cu-Csi-020 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM20
-
 Cu-Csi-021
Cu-Csi-021 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM21
-
 Cu-Csi-022
Cu-Csi-022 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM22
-
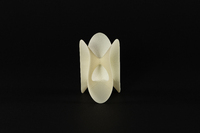 Cu-Csi-023
Cu-Csi-023 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM23
-
 Cu-Csi-024
Cu-Csi-024 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM24
-
 Cu-Csi-025
Cu-Csi-025 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM25
-
 Cu-Csi-026
Cu-Csi-026 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM26
-
 Cu-Csi-027
Cu-Csi-027 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM27
-
 Cu-Csi-028
Cu-Csi-028 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM28
-
 Cu-Csi-029
Cu-Csi-029 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés.
Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987.
Numéro dans la série : KM29
 Ct-Neg-014 Surface de révolution à courbure totale constante négative (type hyperboloïde) version en bois sans lignes géodésiques parallèles et cercles géodésiques.
Ct-Neg-014 Surface de révolution à courbure totale constante négative (type hyperboloïde) version en bois sans lignes géodésiques parallèles et cercles géodésiques. Ct-Neg-015 Plan hyperbolique symétrique crocheté. Donné par Daina Taimina suite à sa visite de la bibliothèque en 2011.
Ct-Neg-015 Plan hyperbolique symétrique crocheté. Donné par Daina Taimina suite à sa visite de la bibliothèque en 2011. Ct-Neg-016 Hélicoïde.
Ct-Neg-016 Hélicoïde. Ct-Neg-017 Deux surfaces de révolution à courbure totale constante négative en tôle de laiton flexible, à l'aide desquelles on peut expliquer le pliage d'une telle surface sur une autre et son déplacement dessus, et plus généralement la notion de "géométrie" sur ces surfaces. S'appliquent sur les modèles numéros 229 (II, 5), 231 (V, 4) et 232 (VIII, 1). Les modèles numéros 229 (II, 5), 231 (V, 4) et 232 (VIII, 1) ont la même courbure. Pour montrer la possibilité de les dérouler l'un sur l'autre et surtout de les déplacer sur eux-mêmes, ainsi que pour montrer les étranges relations entre la géométrie non euclidienne et la géométrie de Lobatschewsky, on les a ajusté sur ces deux bandes de laiton mince. Si l'on découpe dans l'une d'entre elles un morceau triangulaire dont les côtés sont des lignes géodésiques (par exemple celles de la surface 229 (II, 5)), l'observation visuelle nous apprend déjà que la somme des angles dans un tel triangle est inférieure à \(2R\).
Ct-Neg-017 Deux surfaces de révolution à courbure totale constante négative en tôle de laiton flexible, à l'aide desquelles on peut expliquer le pliage d'une telle surface sur une autre et son déplacement dessus, et plus généralement la notion de "géométrie" sur ces surfaces. S'appliquent sur les modèles numéros 229 (II, 5), 231 (V, 4) et 232 (VIII, 1). Les modèles numéros 229 (II, 5), 231 (V, 4) et 232 (VIII, 1) ont la même courbure. Pour montrer la possibilité de les dérouler l'un sur l'autre et surtout de les déplacer sur eux-mêmes, ainsi que pour montrer les étranges relations entre la géométrie non euclidienne et la géométrie de Lobatschewsky, on les a ajusté sur ces deux bandes de laiton mince. Si l'on découpe dans l'une d'entre elles un morceau triangulaire dont les côtés sont des lignes géodésiques (par exemple celles de la surface 229 (II, 5)), l'observation visuelle nous apprend déjà que la somme des angles dans un tel triangle est inférieure à \(2R\). Ct-Pos-001 Surface de révolution de courbure constante positive avec lignes géodésiques. Application sur la sphère, la méridienne ne rencontrant pas l'axe.
Ct-Pos-001 Surface de révolution de courbure constante positive avec lignes géodésiques. Application sur la sphère, la méridienne ne rencontrant pas l'axe. Ct-Pos-002 Surface hélicoïdale de courbure constante positive.
Ct-Pos-002 Surface hélicoïdale de courbure constante positive. Ct-Pos-003 Surface de révolution de courbure constante positive, version en bois sans lignes géodésiques. Application sur la sphère, la méridienne rencontre l'axe.
Ct-Pos-003 Surface de révolution de courbure constante positive, version en bois sans lignes géodésiques. Application sur la sphère, la méridienne rencontre l'axe. Ct-Pos-004 Surface de révolution de courbure constante positive avec lignes géodésiques. Application sur la sphère, la méridienne rencontre l'axe.
Ct-Pos-004 Surface de révolution de courbure constante positive avec lignes géodésiques. Application sur la sphère, la méridienne rencontre l'axe. Ct-Pos-005 Surface hélicoïdale de courbure constante positive.
Ct-Pos-005 Surface hélicoïdale de courbure constante positive. Ct-Pos-006 Surface de révolution de courbure constante positive avec lignes géodésiques. Application sur la sphère, la méridienne ne rencontrant pas l'axe.
Ct-Pos-006 Surface de révolution de courbure constante positive avec lignes géodésiques. Application sur la sphère, la méridienne ne rencontrant pas l'axe. Ct-Pos-007 Demi-sphère creuse en tôle de laiton. Les surfaces à courbure constante, conçues comme une fine peau, peuvent coulisser sur elles-mêmes et se dérouler les unes sur les autres. On peut en faire l'expérience avec les bandes de laiton souples suivantes, ajustées sur ces surfaces. S'applique sur les modèles numéros 220 et 221 (V, 2a et b).
Ct-Pos-007 Demi-sphère creuse en tôle de laiton. Les surfaces à courbure constante, conçues comme une fine peau, peuvent coulisser sur elles-mêmes et se dérouler les unes sur les autres. On peut en faire l'expérience avec les bandes de laiton souples suivantes, ajustées sur ces surfaces. S'applique sur les modèles numéros 220 et 221 (V, 2a et b). Ct-Pos-009 Bande de surface à courbure positive constante en tôle de laiton. Zone sphérique correspondant à un angle centrifuge de presque 90°. Les surfaces à courbure constante, conçues comme une fine peau, peuvent coulisser sur elles-mêmes et se dérouler les unes sur les autres. On peut en faire l'expérience avec les bandes de laiton souples suivantes, ajustées sur ces surfaces. S'applique sur le modèle numéro 222 (V, 2c).
Ct-Pos-009 Bande de surface à courbure positive constante en tôle de laiton. Zone sphérique correspondant à un angle centrifuge de presque 90°. Les surfaces à courbure constante, conçues comme une fine peau, peuvent coulisser sur elles-mêmes et se dérouler les unes sur les autres. On peut en faire l'expérience avec les bandes de laiton souples suivantes, ajustées sur ces surfaces. S'applique sur le modèle numéro 222 (V, 2c). Ct-Reg-001 Hélicoϊde engendré par le développement d'une hélice.
Ct-Reg-001 Hélicoϊde engendré par le développement d'une hélice. Cu-001 Le pentaèdre de Sylvester de la surface diagonale de Clebsch.
Cu-001 Le pentaèdre de Sylvester de la surface diagonale de Clebsch. Cu-002 Surface hessienne du modèle numéro 50 (VII, 7).
Cu-002 Surface hessienne du modèle numéro 50 (VII, 7). Cu-003 Partie étoilée du modèle numéro 64 (VII, 24a) pour un pentaèdre composé du plan infiniment éloigné et d'un tétraèdre régulier.
Cu-003 Partie étoilée du modèle numéro 64 (VII, 24a) pour un pentaèdre composé du plan infiniment éloigné et d'un tétraèdre régulier. Cu-Cne-001 Cône de genre un (de sixième classe), constitué d'une seule enveloppe non appariée en position carrée.
Cu-Cne-001 Cône de genre un (de sixième classe), constitué d'une seule enveloppe non appariée en position carrée. Cu-Cne-002 Cône de genre zéro à double arête (de quatrième classe), qui se présente comme une double arête isolée.
Cu-Cne-002 Cône de genre zéro à double arête (de quatrième classe), qui se présente comme une double arête isolée. Cu-Cne-003 Cône de genre un (de sixième classe), constitué d'une seule enveloppe non appariée avec trois plans de retournement passant par une droite.
Cu-Cne-003 Cône de genre un (de sixième classe), constitué d'une seule enveloppe non appariée avec trois plans de retournement passant par une droite. Cu-Cne-004 Cône de genre zéro avec arête de retour (de troisième classe).
Cu-Cne-004 Cône de genre zéro avec arête de retour (de troisième classe). Cu-Cne-005 Cône de genre un (de sixième classe), constitué d'une enveloppe appariée et d'une enveloppe non appariée.
Cu-Cne-005 Cône de genre un (de sixième classe), constitué d'une enveloppe appariée et d'une enveloppe non appariée. Cu-Cne-006 Cône de genre zéro à double arête (de quatrième classe), avec auto-intersection.
Cu-Cne-006 Cône de genre zéro à double arête (de quatrième classe), avec auto-intersection. Cu-Cne-007 Cône de genre un (de sixième classe), constitué d'une seule enveloppe non appariée en position triangulaire.
Cu-Cne-007 Cône de genre un (de sixième classe), constitué d'une seule enveloppe non appariée en position triangulaire. Cu-Csi-001 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM1
Cu-Csi-001 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM1 Cu-Csi-002 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM2
Cu-Csi-002 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM2 Cu-Csi-003 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM3
Cu-Csi-003 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM3 Cu-Csi-004 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM4
Cu-Csi-004 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM4 Cu-Csi-005 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM5
Cu-Csi-005 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM5 Cu-Csi-006 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM6
Cu-Csi-006 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM6 Cu-Csi-007 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM7
Cu-Csi-007 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM7 Cu-Csi-008 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM8
Cu-Csi-008 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM8 Cu-Csi-009 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM9
Cu-Csi-009 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM9 Cu-Csi-010 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM10
Cu-Csi-010 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM10 Cu-Csi-011 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM11
Cu-Csi-011 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM11 Cu-Csi-012 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM12
Cu-Csi-012 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM12 Cu-Csi-013 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM13
Cu-Csi-013 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM13 Cu-Csi-014 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM14
Cu-Csi-014 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM14 Cu-Csi-015 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM15
Cu-Csi-015 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM15 Cu-Csi-016 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM16
Cu-Csi-016 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM16 Cu-Csi-017 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM17
Cu-Csi-017 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM17 Cu-Csi-018 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM18
Cu-Csi-018 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM18 Cu-Csi-019 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM19
Cu-Csi-019 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM19 Cu-Csi-020 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM20
Cu-Csi-020 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM20 Cu-Csi-021 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM21
Cu-Csi-021 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM21 Cu-Csi-022 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM22
Cu-Csi-022 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM22 Cu-Csi-023 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM23
Cu-Csi-023 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM23 Cu-Csi-024 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM24
Cu-Csi-024 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM24 Cu-Csi-025 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM25
Cu-Csi-025 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM25 Cu-Csi-026 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM26
Cu-Csi-026 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM26 Cu-Csi-027 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM27
Cu-Csi-027 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM27 Cu-Csi-028 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM28
Cu-Csi-028 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM28 Cu-Csi-029 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM29
Cu-Csi-029 Série des 45 types topologiques de surfaces cubiques projectives réelles (non réduites à un cône) à points doubles isolés. Ordonnée selon la classification de Ludwig Schläfli en 1863, et modernisée par Horst Knörrer et Thomas Miller en 1987. Numéro dans la série : KM29