-
 To-Sno-002
To-Sno-002 Ruban de Möbius à bord circulaire.
-
 To-Sno-003
To-Sno-003 Bouteille de Klein en verre.
-
 To-Sno-004
To-Sno-004 Ruban de Möbius en bois.
-
 To-Sno-005
To-Sno-005 Sphère à bonnet croisé. Image du plan projectif avec 2 points pinces.
Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.
-
 To-Sno-006
To-Sno-006 Bonnet croisé. Surface du 4ème ordre avec une droite double : lieu géométrique des cercles de courbure des sections normales d'une surface quelconque dans un élément de surface à courbure positive.
-
 To-Sno-007
To-Sno-007 La surface romaine de Steiner avec des courbes de tangente principale. Elle possède trois droites doubles qui se rejoignent en un point.
-
 To-Sno-008
To-Sno-008 Modèle de la représentation du plan projectif sur une surface sans singularité fermée dans le fini.
Cette surface possède un minimum, un maximum et un maximum minimal et est ainsi la généralisation la plus simple de la sphère en ce qui concerne les extrêmes.
-
 To-Sno-009
To-Sno-009 Surface de Boy. Modèles de la représentation du plan projectif sur une surface fermée sans singularité.
Cette surface possède un axe de symétrie, de sorte que la surface coïncide avec elle-même lors d'une rotation de 120° autour de celle-ci.
-
 To-Sno-010
To-Sno-010 Ruban de Möbius coupé en deux par le milieu formant deux rubans ordinaires enlacés.
-
 To-Sno-011
To-Sno-011 Ruban de Möbius avec alphabet.
-
 To-Sno-012
To-Sno-012 Ruban de Möbius.
-
 To-Sno-013
To-Sno-013 Il s'agit d'une surface du 4ème degré possédant deux singularités du type parapluie de Withney et une ligne double qui est la droite joignant les deux singularités. Cette surface (bonnet croisé) est une image du plan projectif réel avec auto-intersection. Dans son célèbre traité sur les surfaces, Darboux évoque l'impossibilité de représenter le plan projectif dans l'espace euclidien sans auto-intersection. Sa démonstration, quoique très instructive, est incomplète car elle s'appuie sur le fait que la surface cherchée est algébrique.
-
 To-Sno-014
To-Sno-014 Surface romaine de Steiner.
-
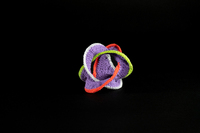 To-Sno-015
To-Sno-015 Surface non orientable bordée par des anneaux borroméens.
Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html).
-
 To-Sno-016
To-Sno-016 Ruban de Möbius (surface non orientable) bordé par un nœud de trèfle.
-
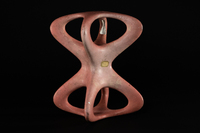 To-Sor-001
To-Sor-001 Surface de genre 6.
-
 To-Sor-002
To-Sor-002 Tore carré plat plongé isométriquement dans l'espace ambiant.
-
 To-Sor-003
To-Sor-003 Carte sur la surface de genre 2 nécessitant 8 couleurs.
-
 To-Sor-004
To-Sor-004 Surface de Morin du huitième degré.
-
 To-Sor-005
To-Sor-005 Surface de genre 3 à symétrie d'ordre 4.
-
 To-Sor-006
To-Sor-006 On trace, dans un plan vertical, une droite verticale et un cercle non centré sur la droite, puis on fait tourner le plan autour de la droite prise comme axe de révolution. Le tore est la surface décrite par le cercle. Par construction le tore contient donc une famille de cercles appelés "méridiens". Lorsque l'on coupe le tore par des plans horizontaux, on trouve une autre famille de cercles appelés "parallèles".
Il existe deux autres familles de cercles sur le tore, les "cercles d'Yvon Villarceau" nommés en hommage à leur découvreur, Antoine Yvon Villarceau. Ils sont obtenus en coupant le tore par un plan bitangent, autrement dit tangent au tore en exactement deux points distincts. On observe alors qu'un tel plan coupe le tore en deux parties égales.
Inversement, est-ce qu'un plan qui coupe le tore en deux parties égales le coupe suivant deux cercles ? La réponse est non, comme le montre ce modèle-ci, sur lequel l'intersection est une courbe de 4ème degré, car le tore lui-même est une surface du 4ème degré.
-
 To-Sor-007
To-Sor-007 On trace, dans un plan vertical, une droite verticale et un cercle non centré sur la droite, puis on fait tourner le plan autour de la droite prise comme axe de révolution. Le tore est la surface décrite par le cercle. Par construction le tore contient donc une famille de cercles appelés "méridiens". Lorsque l'on coupe le tore par des plans horizontaux, on trouve une autre famille de cercles appelés "parallèles".
Il existe deux autres familles de cercles sur le tore, les "cercles d'Yvon Villarceau" nommés en hommage à leur découvreur, Antoine Yvon Villarceau. Ils sont obtenus en coupant le tore par un plan bitangent, autrement dit tangent au tore en exactement deux points distincts, comme sur ce modèle-ci. On observe alors qu'un tel plan coupe le tore en deux parties égales.
Inversement, est-ce qu'un plan qui coupe le tore en deux parties égales le coupe suivant deux cercles ? La réponse est non, l'intersection est alors une courbe de 4ème degré, car le tore lui-même est une surface du 4ème degré.
-
 To-Sor-008
To-Sor-008 Carte complète à 7 couleurs sur un tore.
Réalisé d’après la technique du "bead crochet" (Ellie Baker and Susan Goldstine : Crafting Conundrums / CRC Press, 2014).
-
 To-Sor-009
To-Sor-009 Surface bordée par un entrelacs de trois anneaux.
-
 To-Sor-010
To-Sor-010 Surface de Seifert pour un entrelacs de Hopf (Seifert surface for a Hopf link).
-
 To-Sor-011
To-Sor-011 Surface de Seifert pour des anneaux borroméens.
-
 To-Sor-013
To-Sor-013 Surface de Seifert pour un nœud de trèfle "main gauche" (Seifert surface for a left-handed trefoil).
Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html).
-
 To-Sor-014
To-Sor-014 Surface de Seifert pour un nœud de trèfle "main gauche" (Seifert surface for a left-handed trefoil).
Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html).
-
 To-Sor-015
To-Sor-015 Surface orientable bordée par un nœud de Conway.
-
 To-Sor-016
To-Sor-016 Surface orientable bordée par un nœud à 5 croisements (5_2).
-
 To-Sor-017
To-Sor-017 Surface orientable de genre 1 bordée par un non-nœud.
-
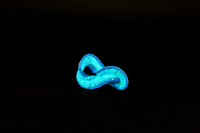 To-Sor-018
To-Sor-018 Surface orientable bordée par un nœud de huit.
-
 Vc-001
Vc-001 Modèle sur la théorie des fonctions.
Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^2=z^2-1 \).
Les deux surfaces R et I qui apparaissent au-dessus du plan \( z \) sont des surfaces de 4ème ordre qui s'étendent en deux nappes au-dessus de ce plan. Les points correspondant à \( z=+1 \) et \( z=-1 \) sont les points de ramification.
-
 Vc-002
Vc-002 Modèle sur la théorie des fonctions.
Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^2=z^2-1 \).
Les deux surfaces R et I qui apparaissent au-dessus du plan \( z \) sont des surfaces de 4ème ordre qui s'étendent en deux nappes au-dessus de ce plan. Les points correspondant à \( z=+1 \) et \( z=-1 \) sont les points de ramification.
-
 Vc-003
Vc-003 Modèle sur la théorie des fonctions.
Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^2=z^4-1 \).
Les surfaces correspondantes, étalées en deux nappes sur le plan \( z \), sont de 8ème ordre et ramifiées en \( z=+1 \), \( z=-1 \), \( z=+i \) et \( z=-i \).
-
 Vc-004
Vc-004 Modèle sur la théorie des fonctions.
Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^2=z^4-1 \).
Les surfaces correspondantes, étalées en deux nappes sur le plan \( z \), sont de 8ème ordre et ramifiées en \( z=+1 \), \( z=-1 \), \( z=+i \) et \( z=-i \).
-
 Vc-005
Vc-005 Modèle sur la théorie des fonctions.
Modèle destiné à illustrer la convergence de deux points logarithmiques infinis en un point algébrique simple.
Pour \( w=\frac1z \).
-
 Vc-006
Vc-006 Modèle sur la théorie des fonctions.
Modèle destiné à illustrer la convergence de deux points logarithmiques infinis en un point algébrique simple.
Pour \( w=\frac{1}{2\varepsilon} \log \frac{z-\varepsilon}{z+\varepsilon}\ \left( \varepsilon= \frac{\pi}{4} \right) \).
-
 Vc-007
Vc-007 Modèle sur la théorie des fonctions.
Le modèle illustre le comportement d'une fonction dans l'environnement du point de singularité essentielle, par \( 6w=e^\frac{1}{6z} \).
\( 6w=e^\frac{1}{6z} \) symbolise le point de singularité essentielle, et la partie réelle de la fonction est représentée par : \( u=\frac{1}{6}e^{x'} \cos y' \) (où \( x'=\frac{x}{6(x^2+y^2)'} \), \(y'=\frac{-y}{6(x^2+y^2)'} \), \( z=x+iy \) est fixé) tandis que la partie imaginaire \( v=\frac{1}{6}e^{x'} \sin y' \) peut être déduite de la première par une transformation du plan \( (x, y) \) par des rayons réciproques.
-
 Vc-008
Vc-008 Partie imaginaire de la fonction ζ (zeta) de Riemann dans le voisinage des dix premiers zéro.
-
 Vc-009
Vc-009 Partie réelle de la fonction ζ (zeta) de Riemann dans le voisinage des dix premiers zéro.
-
 Vc-010
Vc-010 Convexe de Julia-McMullen \(z^2-1\).
-
 Vc-011
Vc-011 Convexe d'Alexandrov-Mandelbrot.
-
 Vc-012
Vc-012 Modèle sur la théorie des fonctions.
Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^4=1-z^2 \).
Pour la fonction w=1. Ici, les deux surfaces R et I sont identiques. On a dans notre représentation une surface s'étendant en quatre feuilles sur le plan \( z \) (du 16ème ordre), pour laquelle chaque fois deux points superposés sont affectés l'un à l'autre comme partie réelle ou imaginaire de la fonction \( w \). Les points \( z=\pm 1 \) sont des points de ramification, dans lesquels les quatre feuilles de la surface sont reliées, en \( z=\infty \) les nappes sont ramifiées par paires.
-
 Vc-Rie-001
Vc-Rie-001 Surface de Riemann à deux feuilles simplement connectées, qui contient un point d'enroulement de 1er degré à l'intérieur.
-
 Vc-Rie-002
Vc-Rie-002 Surface riemannienne triple connexe avec une ligne frontière qui revient à elle-même.
-
 Vc-Rie-003
Vc-Rie-003 Surface de Riemann à trois feuilles simplement connectées, qui contient un point d'enroulement de 2ème degré à l'intérieur.
-
 Vc-Wei-001
Vc-Wei-001 Modèle sur la théorie des fonctions.
Le modèle illustre l'évolution de la fonction elliptique \( w=p(u) \) (dans la forme normale de Weierstrass) pour les invariants \( g_2=4 \), \( g_3=0 \).
-
 Vc-Wei-002
Vc-Wei-002 Modèle sur la théorie des fonctions.
Le modèle illustre l'évolution de la fonction elliptique \( w=p'(u) \) (dans la forme normale de Weierstrass) pour les invariants \( g_2=4 \), \( g_3=0 \).
-
 Vc-Wei-003
Vc-Wei-003 Modèle sur la théorie des fonctions.
Le modèle illustre l'évolution de la fonction elliptique \( w=p(u) \) (dans la forme normale de Weierstrass) pour les invariants \( g_2=0 \), \( g_3=4 \).
-
 Vc-Wei-004
Vc-Wei-004 Modèle sur la théorie des fonctions.
Le modèle illustre l'évolution de la fonction elliptique \( w=p'(u) \) (dans la forme normale de Weierstrass) pour les invariants \( g_2=0 \), \( g_3=4 \).
-
 Vc-Wei-005
Vc-Wei-005 Partie imaginaire de la dérivée de la fonction ℘ de Weierstrass.
 To-Sno-002 Ruban de Möbius à bord circulaire.
To-Sno-002 Ruban de Möbius à bord circulaire. To-Sno-003 Bouteille de Klein en verre.
To-Sno-003 Bouteille de Klein en verre. To-Sno-004 Ruban de Möbius en bois.
To-Sno-004 Ruban de Möbius en bois. To-Sno-005 Sphère à bonnet croisé. Image du plan projectif avec 2 points pinces. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.
To-Sno-005 Sphère à bonnet croisé. Image du plan projectif avec 2 points pinces. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick. To-Sno-006 Bonnet croisé. Surface du 4ème ordre avec une droite double : lieu géométrique des cercles de courbure des sections normales d'une surface quelconque dans un élément de surface à courbure positive.
To-Sno-006 Bonnet croisé. Surface du 4ème ordre avec une droite double : lieu géométrique des cercles de courbure des sections normales d'une surface quelconque dans un élément de surface à courbure positive. To-Sno-007 La surface romaine de Steiner avec des courbes de tangente principale. Elle possède trois droites doubles qui se rejoignent en un point.
To-Sno-007 La surface romaine de Steiner avec des courbes de tangente principale. Elle possède trois droites doubles qui se rejoignent en un point. To-Sno-008 Modèle de la représentation du plan projectif sur une surface sans singularité fermée dans le fini. Cette surface possède un minimum, un maximum et un maximum minimal et est ainsi la généralisation la plus simple de la sphère en ce qui concerne les extrêmes.
To-Sno-008 Modèle de la représentation du plan projectif sur une surface sans singularité fermée dans le fini. Cette surface possède un minimum, un maximum et un maximum minimal et est ainsi la généralisation la plus simple de la sphère en ce qui concerne les extrêmes. To-Sno-009 Surface de Boy. Modèles de la représentation du plan projectif sur une surface fermée sans singularité. Cette surface possède un axe de symétrie, de sorte que la surface coïncide avec elle-même lors d'une rotation de 120° autour de celle-ci.
To-Sno-009 Surface de Boy. Modèles de la représentation du plan projectif sur une surface fermée sans singularité. Cette surface possède un axe de symétrie, de sorte que la surface coïncide avec elle-même lors d'une rotation de 120° autour de celle-ci. To-Sno-010 Ruban de Möbius coupé en deux par le milieu formant deux rubans ordinaires enlacés.
To-Sno-010 Ruban de Möbius coupé en deux par le milieu formant deux rubans ordinaires enlacés. To-Sno-011 Ruban de Möbius avec alphabet.
To-Sno-011 Ruban de Möbius avec alphabet. To-Sno-012 Ruban de Möbius.
To-Sno-012 Ruban de Möbius. To-Sno-013 Il s'agit d'une surface du 4ème degré possédant deux singularités du type parapluie de Withney et une ligne double qui est la droite joignant les deux singularités. Cette surface (bonnet croisé) est une image du plan projectif réel avec auto-intersection. Dans son célèbre traité sur les surfaces, Darboux évoque l'impossibilité de représenter le plan projectif dans l'espace euclidien sans auto-intersection. Sa démonstration, quoique très instructive, est incomplète car elle s'appuie sur le fait que la surface cherchée est algébrique.
To-Sno-013 Il s'agit d'une surface du 4ème degré possédant deux singularités du type parapluie de Withney et une ligne double qui est la droite joignant les deux singularités. Cette surface (bonnet croisé) est une image du plan projectif réel avec auto-intersection. Dans son célèbre traité sur les surfaces, Darboux évoque l'impossibilité de représenter le plan projectif dans l'espace euclidien sans auto-intersection. Sa démonstration, quoique très instructive, est incomplète car elle s'appuie sur le fait que la surface cherchée est algébrique. To-Sno-014 Surface romaine de Steiner.
To-Sno-014 Surface romaine de Steiner. To-Sno-015 Surface non orientable bordée par des anneaux borroméens. Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html).
To-Sno-015 Surface non orientable bordée par des anneaux borroméens. Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html). To-Sno-016 Ruban de Möbius (surface non orientable) bordé par un nœud de trèfle.
To-Sno-016 Ruban de Möbius (surface non orientable) bordé par un nœud de trèfle. To-Sor-001 Surface de genre 6.
To-Sor-001 Surface de genre 6. To-Sor-002 Tore carré plat plongé isométriquement dans l'espace ambiant.
To-Sor-002 Tore carré plat plongé isométriquement dans l'espace ambiant. To-Sor-003 Carte sur la surface de genre 2 nécessitant 8 couleurs.
To-Sor-003 Carte sur la surface de genre 2 nécessitant 8 couleurs. To-Sor-004 Surface de Morin du huitième degré.
To-Sor-004 Surface de Morin du huitième degré. To-Sor-005 Surface de genre 3 à symétrie d'ordre 4.
To-Sor-005 Surface de genre 3 à symétrie d'ordre 4. To-Sor-006 On trace, dans un plan vertical, une droite verticale et un cercle non centré sur la droite, puis on fait tourner le plan autour de la droite prise comme axe de révolution. Le tore est la surface décrite par le cercle. Par construction le tore contient donc une famille de cercles appelés "méridiens". Lorsque l'on coupe le tore par des plans horizontaux, on trouve une autre famille de cercles appelés "parallèles". Il existe deux autres familles de cercles sur le tore, les "cercles d'Yvon Villarceau" nommés en hommage à leur découvreur, Antoine Yvon Villarceau. Ils sont obtenus en coupant le tore par un plan bitangent, autrement dit tangent au tore en exactement deux points distincts. On observe alors qu'un tel plan coupe le tore en deux parties égales. Inversement, est-ce qu'un plan qui coupe le tore en deux parties égales le coupe suivant deux cercles ? La réponse est non, comme le montre ce modèle-ci, sur lequel l'intersection est une courbe de 4ème degré, car le tore lui-même est une surface du 4ème degré.
To-Sor-006 On trace, dans un plan vertical, une droite verticale et un cercle non centré sur la droite, puis on fait tourner le plan autour de la droite prise comme axe de révolution. Le tore est la surface décrite par le cercle. Par construction le tore contient donc une famille de cercles appelés "méridiens". Lorsque l'on coupe le tore par des plans horizontaux, on trouve une autre famille de cercles appelés "parallèles". Il existe deux autres familles de cercles sur le tore, les "cercles d'Yvon Villarceau" nommés en hommage à leur découvreur, Antoine Yvon Villarceau. Ils sont obtenus en coupant le tore par un plan bitangent, autrement dit tangent au tore en exactement deux points distincts. On observe alors qu'un tel plan coupe le tore en deux parties égales. Inversement, est-ce qu'un plan qui coupe le tore en deux parties égales le coupe suivant deux cercles ? La réponse est non, comme le montre ce modèle-ci, sur lequel l'intersection est une courbe de 4ème degré, car le tore lui-même est une surface du 4ème degré. To-Sor-007 On trace, dans un plan vertical, une droite verticale et un cercle non centré sur la droite, puis on fait tourner le plan autour de la droite prise comme axe de révolution. Le tore est la surface décrite par le cercle. Par construction le tore contient donc une famille de cercles appelés "méridiens". Lorsque l'on coupe le tore par des plans horizontaux, on trouve une autre famille de cercles appelés "parallèles". Il existe deux autres familles de cercles sur le tore, les "cercles d'Yvon Villarceau" nommés en hommage à leur découvreur, Antoine Yvon Villarceau. Ils sont obtenus en coupant le tore par un plan bitangent, autrement dit tangent au tore en exactement deux points distincts, comme sur ce modèle-ci. On observe alors qu'un tel plan coupe le tore en deux parties égales. Inversement, est-ce qu'un plan qui coupe le tore en deux parties égales le coupe suivant deux cercles ? La réponse est non, l'intersection est alors une courbe de 4ème degré, car le tore lui-même est une surface du 4ème degré.
To-Sor-007 On trace, dans un plan vertical, une droite verticale et un cercle non centré sur la droite, puis on fait tourner le plan autour de la droite prise comme axe de révolution. Le tore est la surface décrite par le cercle. Par construction le tore contient donc une famille de cercles appelés "méridiens". Lorsque l'on coupe le tore par des plans horizontaux, on trouve une autre famille de cercles appelés "parallèles". Il existe deux autres familles de cercles sur le tore, les "cercles d'Yvon Villarceau" nommés en hommage à leur découvreur, Antoine Yvon Villarceau. Ils sont obtenus en coupant le tore par un plan bitangent, autrement dit tangent au tore en exactement deux points distincts, comme sur ce modèle-ci. On observe alors qu'un tel plan coupe le tore en deux parties égales. Inversement, est-ce qu'un plan qui coupe le tore en deux parties égales le coupe suivant deux cercles ? La réponse est non, l'intersection est alors une courbe de 4ème degré, car le tore lui-même est une surface du 4ème degré. To-Sor-008 Carte complète à 7 couleurs sur un tore. Réalisé d’après la technique du "bead crochet" (Ellie Baker and Susan Goldstine : Crafting Conundrums / CRC Press, 2014).
To-Sor-008 Carte complète à 7 couleurs sur un tore. Réalisé d’après la technique du "bead crochet" (Ellie Baker and Susan Goldstine : Crafting Conundrums / CRC Press, 2014). To-Sor-009 Surface bordée par un entrelacs de trois anneaux.
To-Sor-009 Surface bordée par un entrelacs de trois anneaux. To-Sor-010 Surface de Seifert pour un entrelacs de Hopf (Seifert surface for a Hopf link).
To-Sor-010 Surface de Seifert pour un entrelacs de Hopf (Seifert surface for a Hopf link). To-Sor-011 Surface de Seifert pour des anneaux borroméens.
To-Sor-011 Surface de Seifert pour des anneaux borroméens. To-Sor-013 Surface de Seifert pour un nœud de trèfle "main gauche" (Seifert surface for a left-handed trefoil). Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html).
To-Sor-013 Surface de Seifert pour un nœud de trèfle "main gauche" (Seifert surface for a left-handed trefoil). Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html). To-Sor-014 Surface de Seifert pour un nœud de trèfle "main gauche" (Seifert surface for a left-handed trefoil). Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html).
To-Sor-014 Surface de Seifert pour un nœud de trèfle "main gauche" (Seifert surface for a left-handed trefoil). Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html). To-Sor-015 Surface orientable bordée par un nœud de Conway.
To-Sor-015 Surface orientable bordée par un nœud de Conway. To-Sor-016 Surface orientable bordée par un nœud à 5 croisements (5_2).
To-Sor-016 Surface orientable bordée par un nœud à 5 croisements (5_2). To-Sor-017 Surface orientable de genre 1 bordée par un non-nœud.
To-Sor-017 Surface orientable de genre 1 bordée par un non-nœud. To-Sor-018 Surface orientable bordée par un nœud de huit.
To-Sor-018 Surface orientable bordée par un nœud de huit. Vc-001 Modèle sur la théorie des fonctions. Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^2=z^2-1 \). Les deux surfaces R et I qui apparaissent au-dessus du plan \( z \) sont des surfaces de 4ème ordre qui s'étendent en deux nappes au-dessus de ce plan. Les points correspondant à \( z=+1 \) et \( z=-1 \) sont les points de ramification.
Vc-001 Modèle sur la théorie des fonctions. Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^2=z^2-1 \). Les deux surfaces R et I qui apparaissent au-dessus du plan \( z \) sont des surfaces de 4ème ordre qui s'étendent en deux nappes au-dessus de ce plan. Les points correspondant à \( z=+1 \) et \( z=-1 \) sont les points de ramification. Vc-002 Modèle sur la théorie des fonctions. Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^2=z^2-1 \). Les deux surfaces R et I qui apparaissent au-dessus du plan \( z \) sont des surfaces de 4ème ordre qui s'étendent en deux nappes au-dessus de ce plan. Les points correspondant à \( z=+1 \) et \( z=-1 \) sont les points de ramification.
Vc-002 Modèle sur la théorie des fonctions. Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^2=z^2-1 \). Les deux surfaces R et I qui apparaissent au-dessus du plan \( z \) sont des surfaces de 4ème ordre qui s'étendent en deux nappes au-dessus de ce plan. Les points correspondant à \( z=+1 \) et \( z=-1 \) sont les points de ramification. Vc-003 Modèle sur la théorie des fonctions. Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^2=z^4-1 \). Les surfaces correspondantes, étalées en deux nappes sur le plan \( z \), sont de 8ème ordre et ramifiées en \( z=+1 \), \( z=-1 \), \( z=+i \) et \( z=-i \).
Vc-003 Modèle sur la théorie des fonctions. Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^2=z^4-1 \). Les surfaces correspondantes, étalées en deux nappes sur le plan \( z \), sont de 8ème ordre et ramifiées en \( z=+1 \), \( z=-1 \), \( z=+i \) et \( z=-i \). Vc-004 Modèle sur la théorie des fonctions. Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^2=z^4-1 \). Les surfaces correspondantes, étalées en deux nappes sur le plan \( z \), sont de 8ème ordre et ramifiées en \( z=+1 \), \( z=-1 \), \( z=+i \) et \( z=-i \).
Vc-004 Modèle sur la théorie des fonctions. Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^2=z^4-1 \). Les surfaces correspondantes, étalées en deux nappes sur le plan \( z \), sont de 8ème ordre et ramifiées en \( z=+1 \), \( z=-1 \), \( z=+i \) et \( z=-i \). Vc-005 Modèle sur la théorie des fonctions. Modèle destiné à illustrer la convergence de deux points logarithmiques infinis en un point algébrique simple. Pour \( w=\frac1z \).
Vc-005 Modèle sur la théorie des fonctions. Modèle destiné à illustrer la convergence de deux points logarithmiques infinis en un point algébrique simple. Pour \( w=\frac1z \). Vc-006 Modèle sur la théorie des fonctions. Modèle destiné à illustrer la convergence de deux points logarithmiques infinis en un point algébrique simple. Pour \( w=\frac{1}{2\varepsilon} \log \frac{z-\varepsilon}{z+\varepsilon}\ \left( \varepsilon= \frac{\pi}{4} \right) \).
Vc-006 Modèle sur la théorie des fonctions. Modèle destiné à illustrer la convergence de deux points logarithmiques infinis en un point algébrique simple. Pour \( w=\frac{1}{2\varepsilon} \log \frac{z-\varepsilon}{z+\varepsilon}\ \left( \varepsilon= \frac{\pi}{4} \right) \). Vc-007 Modèle sur la théorie des fonctions. Le modèle illustre le comportement d'une fonction dans l'environnement du point de singularité essentielle, par \( 6w=e^\frac{1}{6z} \). \( 6w=e^\frac{1}{6z} \) symbolise le point de singularité essentielle, et la partie réelle de la fonction est représentée par : \( u=\frac{1}{6}e^{x'} \cos y' \) (où \( x'=\frac{x}{6(x^2+y^2)'} \), \(y'=\frac{-y}{6(x^2+y^2)'} \), \( z=x+iy \) est fixé) tandis que la partie imaginaire \( v=\frac{1}{6}e^{x'} \sin y' \) peut être déduite de la première par une transformation du plan \( (x, y) \) par des rayons réciproques.
Vc-007 Modèle sur la théorie des fonctions. Le modèle illustre le comportement d'une fonction dans l'environnement du point de singularité essentielle, par \( 6w=e^\frac{1}{6z} \). \( 6w=e^\frac{1}{6z} \) symbolise le point de singularité essentielle, et la partie réelle de la fonction est représentée par : \( u=\frac{1}{6}e^{x'} \cos y' \) (où \( x'=\frac{x}{6(x^2+y^2)'} \), \(y'=\frac{-y}{6(x^2+y^2)'} \), \( z=x+iy \) est fixé) tandis que la partie imaginaire \( v=\frac{1}{6}e^{x'} \sin y' \) peut être déduite de la première par une transformation du plan \( (x, y) \) par des rayons réciproques. Vc-008 Partie imaginaire de la fonction ζ (zeta) de Riemann dans le voisinage des dix premiers zéro.
Vc-008 Partie imaginaire de la fonction ζ (zeta) de Riemann dans le voisinage des dix premiers zéro. Vc-009 Partie réelle de la fonction ζ (zeta) de Riemann dans le voisinage des dix premiers zéro.
Vc-009 Partie réelle de la fonction ζ (zeta) de Riemann dans le voisinage des dix premiers zéro. Vc-010 Convexe de Julia-McMullen \(z^2-1\).
Vc-010 Convexe de Julia-McMullen \(z^2-1\). Vc-011 Convexe d'Alexandrov-Mandelbrot.
Vc-011 Convexe d'Alexandrov-Mandelbrot. Vc-012 Modèle sur la théorie des fonctions. Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^4=1-z^2 \). Pour la fonction w=1. Ici, les deux surfaces R et I sont identiques. On a dans notre représentation une surface s'étendant en quatre feuilles sur le plan \( z \) (du 16ème ordre), pour laquelle chaque fois deux points superposés sont affectés l'un à l'autre comme partie réelle ou imaginaire de la fonction \( w \). Les points \( z=\pm 1 \) sont des points de ramification, dans lesquels les quatre feuilles de la surface sont reliées, en \( z=\infty \) les nappes sont ramifiées par paires.
Vc-012 Modèle sur la théorie des fonctions. Le modèle illustre le comportement d'une fonction à proximité de points de ramification : pour la fonction \( w^4=1-z^2 \). Pour la fonction w=1. Ici, les deux surfaces R et I sont identiques. On a dans notre représentation une surface s'étendant en quatre feuilles sur le plan \( z \) (du 16ème ordre), pour laquelle chaque fois deux points superposés sont affectés l'un à l'autre comme partie réelle ou imaginaire de la fonction \( w \). Les points \( z=\pm 1 \) sont des points de ramification, dans lesquels les quatre feuilles de la surface sont reliées, en \( z=\infty \) les nappes sont ramifiées par paires. Vc-Rie-001 Surface de Riemann à deux feuilles simplement connectées, qui contient un point d'enroulement de 1er degré à l'intérieur.
Vc-Rie-001 Surface de Riemann à deux feuilles simplement connectées, qui contient un point d'enroulement de 1er degré à l'intérieur. Vc-Rie-002 Surface riemannienne triple connexe avec une ligne frontière qui revient à elle-même.
Vc-Rie-002 Surface riemannienne triple connexe avec une ligne frontière qui revient à elle-même. Vc-Rie-003 Surface de Riemann à trois feuilles simplement connectées, qui contient un point d'enroulement de 2ème degré à l'intérieur.
Vc-Rie-003 Surface de Riemann à trois feuilles simplement connectées, qui contient un point d'enroulement de 2ème degré à l'intérieur. Vc-Wei-001 Modèle sur la théorie des fonctions. Le modèle illustre l'évolution de la fonction elliptique \( w=p(u) \) (dans la forme normale de Weierstrass) pour les invariants \( g_2=4 \), \( g_3=0 \).
Vc-Wei-001 Modèle sur la théorie des fonctions. Le modèle illustre l'évolution de la fonction elliptique \( w=p(u) \) (dans la forme normale de Weierstrass) pour les invariants \( g_2=4 \), \( g_3=0 \). Vc-Wei-002 Modèle sur la théorie des fonctions. Le modèle illustre l'évolution de la fonction elliptique \( w=p'(u) \) (dans la forme normale de Weierstrass) pour les invariants \( g_2=4 \), \( g_3=0 \).
Vc-Wei-002 Modèle sur la théorie des fonctions. Le modèle illustre l'évolution de la fonction elliptique \( w=p'(u) \) (dans la forme normale de Weierstrass) pour les invariants \( g_2=4 \), \( g_3=0 \). Vc-Wei-003 Modèle sur la théorie des fonctions. Le modèle illustre l'évolution de la fonction elliptique \( w=p(u) \) (dans la forme normale de Weierstrass) pour les invariants \( g_2=0 \), \( g_3=4 \).
Vc-Wei-003 Modèle sur la théorie des fonctions. Le modèle illustre l'évolution de la fonction elliptique \( w=p(u) \) (dans la forme normale de Weierstrass) pour les invariants \( g_2=0 \), \( g_3=4 \). Vc-Wei-004 Modèle sur la théorie des fonctions. Le modèle illustre l'évolution de la fonction elliptique \( w=p'(u) \) (dans la forme normale de Weierstrass) pour les invariants \( g_2=0 \), \( g_3=4 \).
Vc-Wei-004 Modèle sur la théorie des fonctions. Le modèle illustre l'évolution de la fonction elliptique \( w=p'(u) \) (dans la forme normale de Weierstrass) pour les invariants \( g_2=0 \), \( g_3=4 \). Vc-Wei-005 Partie imaginaire de la dérivée de la fonction ℘ de Weierstrass.
Vc-Wei-005 Partie imaginaire de la dérivée de la fonction ℘ de Weierstrass.