-
 Qt-004
Qt-004 Surface du 4ème degré à 9 points doubles réels.
-
 Qt-005
Qt-005 Surface du 4ème degré à une pointe.
$$y^4+y^2(2x^2+3ax+2z^2+az)+x^4-ax^3+x^2(2z^2+az)+z(z-a)^3= 0$$
-
 Qt-006
Qt-006 Surface hyper elliptique du 4ème degré 32 droites.
-
 Qt-007
Qt-007 \( \sum(y^zz^a)-2xyz\sum(x)+4a(y-z)(z-x)(x-y)+4a^2\sum(x^2)-10a^a\sum(yz)-27a^4=0 \)
L'arrête de rebroussement est la cubique \( y=\frac{a(x-3a)}{x+a} \) \( z=-\frac{a(x+3a)}{x-a} \) dont les symptotes sont trois arrêtes d'un cercle.
-
 Qt-008
Qt-008 Surface quartique appelée surface de Cassini, avec ovales de Cassini tracés.
-
 Qt-009
Qt-009 Voûte bohémienne. Surface du 4ème degré avec deux droites doubles sécantes.
-
 Qt-Kum-001
Qt-Kum-001 Surface de Kummer à quatre points doubles réels.
-
 Qt-Kum-002
Qt-Kum-002 Surface de Kummer à seize points doubles réels.
-
 Qt-Kum-003
Qt-Kum-003 Surface de Kummer à huit points doubles réels.
-
 Qt-Kum-004
Qt-Kum-004 Surface du 4ème ordre avec quatre plans qui se touchent dans le sens de la longueur des cercles.
La surface est composée de dix (six et quatre congruents entre eux), qui sont reliées par douze nœuds coniques.
-
 Qt-Kum-005
Qt-Kum-005 Surface du 4ème ordre avec quatre plans qui se touchent dans le sens de la longueur des cercles.
La surface se compose de six parties congruentes, reliées entre elles par quatre nœuds uniplanaires.
-
 Qt-Kum-006
Qt-Kum-006 Surface du 4ème ordre avec quatre plans qui se touchent dans le sens de la longueur des cercles.
La surface se compose de quatre parties congruentes, reliées entre elles par quatre nœuds uniplanaires.
-
 Qt-Kum-010
Qt-Kum-010 Surface de Kummer.
-
 Qt-Kum-011
Qt-Kum-011 Surface de Kummer 12 points doubles réels.
-
 Qt-Kum-012
Qt-Kum-012 Surfaces du 4ème degré, lieu des points dont la somme des distances à deux droites est constante.
-
 Qt-Kum-013
Qt-Kum-013 Surface du 4ème degré à 12 points doubles réels.
-
 Qt-Kum-014
Qt-Kum-014 Surface du 4ème degré à 12 points doubles réels, et 3 à l'infini.
-
 Qt-Reg-001
Qt-Reg-001 Surface réglée du 4° ordre cubique double sans point pince.
-
 Qt-Reg-002
Qt-Reg-002 Surface réglée du 4° ordre 1 droite triple (conoïde).
-
 Qt-Reg-003
Qt-Reg-003 Surface réglée du 4° ordre cubique double.
-
 Qt-Reg-006
Qt-Reg-006 Surface réglée du 4° ordre, lieu d'une droite dont 2 points décrivent 2 droites rectangulaires.
-
 Qt-Reg-007
Qt-Reg-007 Surface réglée du 4° ordre, lieu d'une droite dont 2 points décrivent 2 droites rectangulaires.
Surface gauche lieu d'une droite dont deux points décrivent deux axes rectangulaires.
-
 Qt-Reg-008
Qt-Reg-008 Surface réglée du 4ème ordre, lieu des normales à une section de cône de révolution.
-
 Qt-Reg-009
Qt-Reg-009 Surface réglée du 4ème degré, hyperboloïde conchoïdal de Catalan (Muret 162).
-
 Qt-Reg-011
Qt-Reg-011 Surface réglée du 4ème ordre.
Surface réglée avec deux droites doubles réelles et quatre points pinces. Elle se compose de deux parties, sur chacune desquelles se trouve un morceau de chaque droite double.
-
 Qt-Reg-013
Qt-Reg-013 Surface réglée du 4ème ordre.
Surface réglée avec deux droites doubles réelles et quatre points pinces sur l'une d'elles. Les deux enveloppes de cette surface contiennent chacune un morceau d'une double droite et se coupent mutuellement le long de l'autre.
-
 Qt-Reg-014
Qt-Reg-014 Surface réglée du 4ème ordre.
Surface réglée avec deux droites doubles imaginaires conjuguées ; elle est constituée de deux parties de surface hyperpoloïdes.
-
 Qt-Reg-016
Qt-Reg-016 Surface réglée du 4ème ordre.
Surface réglée avec une droite triple et quatre points pinces sur celle-ci ; cette surface possède encore une droite directrice simple.
-
 Qt-Reg-017
Qt-Reg-017 Surface réglée du 4ème ordre.
Surface réglée avec une triple droite et deux plans tangents constants le long de celle-ci ; c'est-à-dire que la génératrice qui décrit la surface passe deux fois par la position de la triple droite. Il y a deux points singuliers supérieurs sur la triple droite.
-
 Qt-Reg-019
Qt-Reg-019 Surface réglée du 4ème ordre.
Surface réglée avec une double courbe du 3ème ordre et quatre points pinces. Elle est constituée d'une seule partie de surface, formée de doubles sécants réels et idéaux de la courbe gauche du 3ème ordre. La surface comprend quatre tangentes à la courbe gauche, qui forment la transition entre les sécants réels et idéaux.
-
 Qt-Reg-020
Qt-Reg-020 Surface réglée du 4ème ordre.
Surface réglée avec une double courbe du 3ème ordre sans points pinces. Elle est formée de doubles sécantes réelles et idéales de la courbe gauche du 3ème ordre, et ce sont à nouveau quatre tangentes de la courbe gauche qui forment la transition. La surface est constituée d'une seule partie qui s'étend le long de toute la courbe double.
-
 Sg-001
Sg-001 Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc.
-
 Sg-002
Sg-002 Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc.
-
 Sg-Lgc-001
Sg-Lgc-001 Surface de largeur constante.
Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton.
On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé (celui-ci), un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux.
-
 Sg-Lgc-002
Sg-Lgc-002 Surface de largeur constante.
Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton.
On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux (celui-ci).
-
 Sg-Lgc-003
Sg-Lgc-003 Surface de largeur constante.
Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton.
On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie (celui-ci), le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux .
-
 Sg-Sta-001
Sg-Sta-001 Gömböc 1928.
-
 Sg-Sta-002
Sg-Sta-002 Gömböc en plexiglass.
-
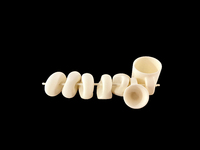 To-001
To-001 Topology joke. "La blague traditionnelle sur les topologues est qu'ils ne peuvent pas faire la différence entre une tasse à café et un donut (ou si vous préférez, un beignet)."
Surface obtenue en déformant continûment un tore : transformation de la tasse à la bouée.
-
 To-002
To-002 Topologie, le tore unilatère de Klein.
Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.
-
 To-003
To-003 Topologie : analysis situs (étude de connexions).
-
 To-004
To-004 Topologie : tore coupé.
-
 To-005
To-005 Topologie : cylindres.
-
 To-006
To-006 Topologie : morceaux de sphères.
-
 To-007
To-007 Topologie : morceaux de sphères.
-
 To-008
To-008 Topologie : morceaux de sphères.
-
 To-009
To-009 Topologie : assemblages de parallélépipèdes.
-
 To-010
To-010 Topologie : morceaux de tores.
-
 To-011
To-011 Topologie : morceaux de tores.
-
 To-012
To-012 Topologie : tore.
-
 To-013
To-013 Topologie : morceaux de sphères.
-
 To-Sno-001
To-Sno-001 Cyclide unilatère.
Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.
 Qt-004 Surface du 4ème degré à 9 points doubles réels.
Qt-004 Surface du 4ème degré à 9 points doubles réels. Qt-005 Surface du 4ème degré à une pointe. $$y^4+y^2(2x^2+3ax+2z^2+az)+x^4-ax^3+x^2(2z^2+az)+z(z-a)^3= 0$$
Qt-005 Surface du 4ème degré à une pointe. $$y^4+y^2(2x^2+3ax+2z^2+az)+x^4-ax^3+x^2(2z^2+az)+z(z-a)^3= 0$$ Qt-006 Surface hyper elliptique du 4ème degré 32 droites.
Qt-006 Surface hyper elliptique du 4ème degré 32 droites. Qt-007 \( \sum(y^zz^a)-2xyz\sum(x)+4a(y-z)(z-x)(x-y)+4a^2\sum(x^2)-10a^a\sum(yz)-27a^4=0 \) L'arrête de rebroussement est la cubique \( y=\frac{a(x-3a)}{x+a} \) \( z=-\frac{a(x+3a)}{x-a} \) dont les symptotes sont trois arrêtes d'un cercle.
Qt-007 \( \sum(y^zz^a)-2xyz\sum(x)+4a(y-z)(z-x)(x-y)+4a^2\sum(x^2)-10a^a\sum(yz)-27a^4=0 \) L'arrête de rebroussement est la cubique \( y=\frac{a(x-3a)}{x+a} \) \( z=-\frac{a(x+3a)}{x-a} \) dont les symptotes sont trois arrêtes d'un cercle. Qt-008 Surface quartique appelée surface de Cassini, avec ovales de Cassini tracés.
Qt-008 Surface quartique appelée surface de Cassini, avec ovales de Cassini tracés. Qt-009 Voûte bohémienne. Surface du 4ème degré avec deux droites doubles sécantes.
Qt-009 Voûte bohémienne. Surface du 4ème degré avec deux droites doubles sécantes. Qt-Kum-001 Surface de Kummer à quatre points doubles réels.
Qt-Kum-001 Surface de Kummer à quatre points doubles réels. Qt-Kum-002 Surface de Kummer à seize points doubles réels.
Qt-Kum-002 Surface de Kummer à seize points doubles réels. Qt-Kum-003 Surface de Kummer à huit points doubles réels.
Qt-Kum-003 Surface de Kummer à huit points doubles réels. Qt-Kum-004 Surface du 4ème ordre avec quatre plans qui se touchent dans le sens de la longueur des cercles. La surface est composée de dix (six et quatre congruents entre eux), qui sont reliées par douze nœuds coniques.
Qt-Kum-004 Surface du 4ème ordre avec quatre plans qui se touchent dans le sens de la longueur des cercles. La surface est composée de dix (six et quatre congruents entre eux), qui sont reliées par douze nœuds coniques. Qt-Kum-005 Surface du 4ème ordre avec quatre plans qui se touchent dans le sens de la longueur des cercles. La surface se compose de six parties congruentes, reliées entre elles par quatre nœuds uniplanaires.
Qt-Kum-005 Surface du 4ème ordre avec quatre plans qui se touchent dans le sens de la longueur des cercles. La surface se compose de six parties congruentes, reliées entre elles par quatre nœuds uniplanaires. Qt-Kum-006 Surface du 4ème ordre avec quatre plans qui se touchent dans le sens de la longueur des cercles. La surface se compose de quatre parties congruentes, reliées entre elles par quatre nœuds uniplanaires.
Qt-Kum-006 Surface du 4ème ordre avec quatre plans qui se touchent dans le sens de la longueur des cercles. La surface se compose de quatre parties congruentes, reliées entre elles par quatre nœuds uniplanaires. Qt-Kum-010 Surface de Kummer.
Qt-Kum-010 Surface de Kummer. Qt-Kum-011 Surface de Kummer 12 points doubles réels.
Qt-Kum-011 Surface de Kummer 12 points doubles réels. Qt-Kum-012 Surfaces du 4ème degré, lieu des points dont la somme des distances à deux droites est constante.
Qt-Kum-012 Surfaces du 4ème degré, lieu des points dont la somme des distances à deux droites est constante. Qt-Kum-013 Surface du 4ème degré à 12 points doubles réels.
Qt-Kum-013 Surface du 4ème degré à 12 points doubles réels. Qt-Kum-014 Surface du 4ème degré à 12 points doubles réels, et 3 à l'infini.
Qt-Kum-014 Surface du 4ème degré à 12 points doubles réels, et 3 à l'infini. Qt-Reg-001 Surface réglée du 4° ordre cubique double sans point pince.
Qt-Reg-001 Surface réglée du 4° ordre cubique double sans point pince. Qt-Reg-002 Surface réglée du 4° ordre 1 droite triple (conoïde).
Qt-Reg-002 Surface réglée du 4° ordre 1 droite triple (conoïde). Qt-Reg-003 Surface réglée du 4° ordre cubique double.
Qt-Reg-003 Surface réglée du 4° ordre cubique double. Qt-Reg-006 Surface réglée du 4° ordre, lieu d'une droite dont 2 points décrivent 2 droites rectangulaires.
Qt-Reg-006 Surface réglée du 4° ordre, lieu d'une droite dont 2 points décrivent 2 droites rectangulaires. Qt-Reg-007 Surface réglée du 4° ordre, lieu d'une droite dont 2 points décrivent 2 droites rectangulaires. Surface gauche lieu d'une droite dont deux points décrivent deux axes rectangulaires.
Qt-Reg-007 Surface réglée du 4° ordre, lieu d'une droite dont 2 points décrivent 2 droites rectangulaires. Surface gauche lieu d'une droite dont deux points décrivent deux axes rectangulaires. Qt-Reg-008 Surface réglée du 4ème ordre, lieu des normales à une section de cône de révolution.
Qt-Reg-008 Surface réglée du 4ème ordre, lieu des normales à une section de cône de révolution. Qt-Reg-009 Surface réglée du 4ème degré, hyperboloïde conchoïdal de Catalan (Muret 162).
Qt-Reg-009 Surface réglée du 4ème degré, hyperboloïde conchoïdal de Catalan (Muret 162). Qt-Reg-011 Surface réglée du 4ème ordre. Surface réglée avec deux droites doubles réelles et quatre points pinces. Elle se compose de deux parties, sur chacune desquelles se trouve un morceau de chaque droite double.
Qt-Reg-011 Surface réglée du 4ème ordre. Surface réglée avec deux droites doubles réelles et quatre points pinces. Elle se compose de deux parties, sur chacune desquelles se trouve un morceau de chaque droite double. Qt-Reg-013 Surface réglée du 4ème ordre. Surface réglée avec deux droites doubles réelles et quatre points pinces sur l'une d'elles. Les deux enveloppes de cette surface contiennent chacune un morceau d'une double droite et se coupent mutuellement le long de l'autre.
Qt-Reg-013 Surface réglée du 4ème ordre. Surface réglée avec deux droites doubles réelles et quatre points pinces sur l'une d'elles. Les deux enveloppes de cette surface contiennent chacune un morceau d'une double droite et se coupent mutuellement le long de l'autre. Qt-Reg-014 Surface réglée du 4ème ordre. Surface réglée avec deux droites doubles imaginaires conjuguées ; elle est constituée de deux parties de surface hyperpoloïdes.
Qt-Reg-014 Surface réglée du 4ème ordre. Surface réglée avec deux droites doubles imaginaires conjuguées ; elle est constituée de deux parties de surface hyperpoloïdes. Qt-Reg-016 Surface réglée du 4ème ordre. Surface réglée avec une droite triple et quatre points pinces sur celle-ci ; cette surface possède encore une droite directrice simple.
Qt-Reg-016 Surface réglée du 4ème ordre. Surface réglée avec une droite triple et quatre points pinces sur celle-ci ; cette surface possède encore une droite directrice simple. Qt-Reg-017 Surface réglée du 4ème ordre. Surface réglée avec une triple droite et deux plans tangents constants le long de celle-ci ; c'est-à-dire que la génératrice qui décrit la surface passe deux fois par la position de la triple droite. Il y a deux points singuliers supérieurs sur la triple droite.
Qt-Reg-017 Surface réglée du 4ème ordre. Surface réglée avec une triple droite et deux plans tangents constants le long de celle-ci ; c'est-à-dire que la génératrice qui décrit la surface passe deux fois par la position de la triple droite. Il y a deux points singuliers supérieurs sur la triple droite. Qt-Reg-019 Surface réglée du 4ème ordre. Surface réglée avec une double courbe du 3ème ordre et quatre points pinces. Elle est constituée d'une seule partie de surface, formée de doubles sécants réels et idéaux de la courbe gauche du 3ème ordre. La surface comprend quatre tangentes à la courbe gauche, qui forment la transition entre les sécants réels et idéaux.
Qt-Reg-019 Surface réglée du 4ème ordre. Surface réglée avec une double courbe du 3ème ordre et quatre points pinces. Elle est constituée d'une seule partie de surface, formée de doubles sécants réels et idéaux de la courbe gauche du 3ème ordre. La surface comprend quatre tangentes à la courbe gauche, qui forment la transition entre les sécants réels et idéaux. Qt-Reg-020 Surface réglée du 4ème ordre. Surface réglée avec une double courbe du 3ème ordre sans points pinces. Elle est formée de doubles sécantes réelles et idéales de la courbe gauche du 3ème ordre, et ce sont à nouveau quatre tangentes de la courbe gauche qui forment la transition. La surface est constituée d'une seule partie qui s'étend le long de toute la courbe double.
Qt-Reg-020 Surface réglée du 4ème ordre. Surface réglée avec une double courbe du 3ème ordre sans points pinces. Elle est formée de doubles sécantes réelles et idéales de la courbe gauche du 3ème ordre, et ce sont à nouveau quatre tangentes de la courbe gauche qui forment la transition. La surface est constituée d'une seule partie qui s'étend le long de toute la courbe double. Sg-001 Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc.
Sg-001 Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc. Sg-002 Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc.
Sg-002 Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc. Sg-Lgc-001 Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé (celui-ci), un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux.
Sg-Lgc-001 Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé (celui-ci), un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux. Sg-Lgc-002 Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux (celui-ci).
Sg-Lgc-002 Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux (celui-ci). Sg-Lgc-003 Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie (celui-ci), le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux .
Sg-Lgc-003 Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie (celui-ci), le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux . Sg-Sta-001 Gömböc 1928.
Sg-Sta-001 Gömböc 1928. Sg-Sta-002 Gömböc en plexiglass.
Sg-Sta-002 Gömböc en plexiglass. To-001 Topology joke. "La blague traditionnelle sur les topologues est qu'ils ne peuvent pas faire la différence entre une tasse à café et un donut (ou si vous préférez, un beignet)." Surface obtenue en déformant continûment un tore : transformation de la tasse à la bouée.
To-001 Topology joke. "La blague traditionnelle sur les topologues est qu'ils ne peuvent pas faire la différence entre une tasse à café et un donut (ou si vous préférez, un beignet)." Surface obtenue en déformant continûment un tore : transformation de la tasse à la bouée. To-002 Topologie, le tore unilatère de Klein. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.
To-002 Topologie, le tore unilatère de Klein. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick. To-003 Topologie : analysis situs (étude de connexions).
To-003 Topologie : analysis situs (étude de connexions). To-004 Topologie : tore coupé.
To-004 Topologie : tore coupé. To-005 Topologie : cylindres.
To-005 Topologie : cylindres. To-006 Topologie : morceaux de sphères.
To-006 Topologie : morceaux de sphères. To-007 Topologie : morceaux de sphères.
To-007 Topologie : morceaux de sphères. To-008 Topologie : morceaux de sphères.
To-008 Topologie : morceaux de sphères. To-009 Topologie : assemblages de parallélépipèdes.
To-009 Topologie : assemblages de parallélépipèdes. To-010 Topologie : morceaux de tores.
To-010 Topologie : morceaux de tores. To-011 Topologie : morceaux de tores.
To-011 Topologie : morceaux de tores. To-012 Topologie : tore.
To-012 Topologie : tore. To-013 Topologie : morceaux de sphères.
To-013 Topologie : morceaux de sphères. To-Sno-001 Cyclide unilatère. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.
To-Sno-001 Cyclide unilatère. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.