-
 E139
E139 Spéciale A.
-
 E139.1
E139.1
-
 E139.2
E139.2
-
 E140
E140 Sujet d'épure.
-
 Édouard Goursat
Édouard Goursat Nombre de copies : 1
Don de Roger Mansuy à l'IHP le 22/08/2023.
-
 Ellipsographe Caronnet
Ellipsographe Caronnet Ellipsographe imaginé par M. Caronnet et fabriqué par la Maison Hue, fondée en 1827, C. Coppin successeur.
-
 Ellipsographe Rohn
Ellipsographe Rohn Ellipsographe, par le conseiller privé professeur Dr. Karl Rohn à Leipzig.
Le compas elliptique repose sur le théorème bien connu selon lequel tout point \( P \) d'un segment \( AB \) décrit une ellipse si ce segment est déplacé de telle sorte que ses extrémités \( A \) et \( B \) glissent sur deux droites perpendiculaires \( x \) et \( y \).
-
 Ellipsoïde laqué
Ellipsoïde laqué Ellipsoïde réalisé par tranches successives de contreplaqué assemblées par Pierre Gallais (Lyon), puis couvert d'une laque végétale "urushi" par Martine Rey (Voiron).
-
 Émile Borel
Émile Borel Nombre de copies : 1
-
 Émile Picard
Émile Picard Nombre de copies : 2
Dans un cadre, sous verre.
-
 Évariste Galois
Évariste Galois Nombre de copies : 1
-
 Flexi-calculateur
Flexi-calculateur Flexi-calculateur "Herrera" pour intégrales pour fonction elliptiques.
-
 Gaston Darboux
Gaston Darboux Nombre de copies : 4 bronzes, 2 argents
Les médailles en bronze sont dans un cadre, sous verre.
-
 Gd-002
Gd-002 Surface engendrée par une section plane d'un cylindre qui roule sur un cylindre.
-
 Gd-003
Gd-003 Surface engendrée par une courbe d'un cylindre qui roule sur un plan.
-
 Gd-004
Gd-004 Surface algébrique rationnelle du 8ème degré.
-
 Gd-005
Gd-005 Surface engendrée par une section plane de cylindre qui roule sur un plan.
-
 Gd-006
Gd-006 Surface engendrée par une courbe d'un cylindre qui roule sur un plan.
-
 Gd-007
Gd-007 Surface définie paramétriquement.
-
 Gd-008
Gd-008 Surface définie paramétriquement.
-
 Gd-009
Gd-009 Surface définie paramétriquement.
-
 Gd-010
Gd-010 Surface correspondant à la sphère avec orthogonalité des éléments.
-
 Gd-011
Gd-011 Modèle de l'emplacement des centres des cordes d'une courbe gauche.
-
 Gd-012
Gd-012 Modèle de l'interface du réseau parabolique de rayons.
-
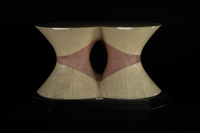 Gd-013
Gd-013 Hyperboloϊde double.
-
 Gd-014
Gd-014 Modèle de la surface \( z=x\ y\ \cdot \frac{x^2-y^2}{x^2+y^2} \), pour son point zéro singulier \( \frac{\delta^2\ z}{\delta\ x\ \delta\ y}\neq \frac{\delta^2\ z}{\delta\ y\ \delta\ x} \).
-
 Gd-015
Gd-015 Modèle d'une surface du 3ème degré, pour expliquer le comportement d'une surface courbe à proximité d'un point parabolique.
-
 Gd-016
Gd-016 Cône sinusoïdale à trois saillies et creux, avec sections horizontales. Cette surface est engendrée par une droite qui glisse sur une courbe sinusoïdale enroulée sur un cylindre et qui passe constamment par un même point situé sur l’axe de ce cylindre.
-
 Gd-017
Gd-017 Surface engendrée par une section plane d'un cylindre qui roule sur un cylindre.
-
 Gd-018
Gd-018 Graphe de la fonction \(z=\frac{x^2y^2}{(x^2+y^2)^{3/2}}\).
-
 Gd-App-001
Gd-App-001 Surface hélicoidale applicable sur l'éllipsoide de révolution, version en bois.
-
 Gd-App-002
Gd-App-002 Surface hélicoidale applicable sur l'éllipsoide de révolution.
-
 Gd-App-003
Gd-App-003 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b).
-
 Gd-App-004
Gd-App-004 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b), version en bois.
-
 Gd-App-005
Gd-App-005 Ellipsoïde de révolution, version en laiton flexible qui s'applique sur le modèle numéro 235 (VIII, 7c).
-
 Gd-App-006
Gd-App-006 Modèle d'une surface développable sur le paraboloïde de révolution de 12ème ordre et 10ème classe.
-
 Gd-App-007
Gd-App-007 Surface applicable sur le paraboloïde de révolution.
-
 Gd-App-008
Gd-App-008 Surface sur laquelle l'ellipsoïde est représenté de manière conforme par des normales parallèles.
-
 Gd-Can-001
Gd-Can-001 Surface canal hélicoϊdale et lignes de courbure.
-
 Gd-Can-002
Gd-Can-002 Surface spirale développée de sphère.
-
 Gd-Can-003
Gd-Can-003 Surface spirale lieu de cercles.
-
 Gd-Can-004
Gd-Can-004 Surface canal engendrée par une sphère de rayon constant.
-
 Gd-Cau-001
Gd-Cau-001 Surface du 12ème degré. Surface caustique des rayons partant d'une ligne lumineuse après leur réflexion sur un cylindre dont l'axe touche la ligne.
-
 Gd-Cau-002
Gd-Cau-002 Enveloppe de normales d'un conoïde de Plϋcker.
-
 Gd-Cau-003
Gd-Cau-003 Enveloppe de normales d'un paraboloïde.
-
 Gd-Cau-004
Gd-Cau-004 Enveloppe de normales d'un hyperboloïde.
-
 Gd-Cau-005
Gd-Cau-005 Enveloppe de normales d'un ellipsoïde.
-
 Gd-Cau-006
Gd-Cau-006 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires.
\(a=16, b=10, c=0\)
\(K=-1\)
-
 Gd-Cau-007
Gd-Cau-007 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires.
\(a=16, b=10, c=0\)
\(K=3\)
-
 Gd-Cau-008
Gd-Cau-008 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires.
\(a=16, b=10, c=0\)
\(K=\frac{b}{3}=\frac{10}{3}\)
-
 Gd-Cau-009
Gd-Cau-009 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires.
\(a=16, b=10, c=0\)
\(K=5,4\)
-
 Gd-Cau-010
Gd-Cau-010 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires.
\(a=16, b=10, c=0\)
\(K=8\)
 E139 Spéciale A.
E139 Spéciale A. E139.1
E139.1
 E139.2
E139.2
 E140 Sujet d'épure.
E140 Sujet d'épure. Édouard Goursat Nombre de copies : 1 Don de Roger Mansuy à l'IHP le 22/08/2023.
Édouard Goursat Nombre de copies : 1 Don de Roger Mansuy à l'IHP le 22/08/2023. Ellipsographe Caronnet Ellipsographe imaginé par M. Caronnet et fabriqué par la Maison Hue, fondée en 1827, C. Coppin successeur.
Ellipsographe Caronnet Ellipsographe imaginé par M. Caronnet et fabriqué par la Maison Hue, fondée en 1827, C. Coppin successeur. Ellipsographe Rohn Ellipsographe, par le conseiller privé professeur Dr. Karl Rohn à Leipzig. Le compas elliptique repose sur le théorème bien connu selon lequel tout point \( P \) d'un segment \( AB \) décrit une ellipse si ce segment est déplacé de telle sorte que ses extrémités \( A \) et \( B \) glissent sur deux droites perpendiculaires \( x \) et \( y \).
Ellipsographe Rohn Ellipsographe, par le conseiller privé professeur Dr. Karl Rohn à Leipzig. Le compas elliptique repose sur le théorème bien connu selon lequel tout point \( P \) d'un segment \( AB \) décrit une ellipse si ce segment est déplacé de telle sorte que ses extrémités \( A \) et \( B \) glissent sur deux droites perpendiculaires \( x \) et \( y \). Ellipsoïde laqué Ellipsoïde réalisé par tranches successives de contreplaqué assemblées par Pierre Gallais (Lyon), puis couvert d'une laque végétale "urushi" par Martine Rey (Voiron).
Ellipsoïde laqué Ellipsoïde réalisé par tranches successives de contreplaqué assemblées par Pierre Gallais (Lyon), puis couvert d'une laque végétale "urushi" par Martine Rey (Voiron). Émile Borel Nombre de copies : 1
Émile Borel Nombre de copies : 1 Émile Picard Nombre de copies : 2 Dans un cadre, sous verre.
Émile Picard Nombre de copies : 2 Dans un cadre, sous verre. Évariste Galois Nombre de copies : 1
Évariste Galois Nombre de copies : 1 Flexi-calculateur Flexi-calculateur "Herrera" pour intégrales pour fonction elliptiques.
Flexi-calculateur Flexi-calculateur "Herrera" pour intégrales pour fonction elliptiques. Gaston Darboux Nombre de copies : 4 bronzes, 2 argents Les médailles en bronze sont dans un cadre, sous verre.
Gaston Darboux Nombre de copies : 4 bronzes, 2 argents Les médailles en bronze sont dans un cadre, sous verre. Gd-002 Surface engendrée par une section plane d'un cylindre qui roule sur un cylindre.
Gd-002 Surface engendrée par une section plane d'un cylindre qui roule sur un cylindre. Gd-003 Surface engendrée par une courbe d'un cylindre qui roule sur un plan.
Gd-003 Surface engendrée par une courbe d'un cylindre qui roule sur un plan. Gd-004 Surface algébrique rationnelle du 8ème degré.
Gd-004 Surface algébrique rationnelle du 8ème degré. Gd-005 Surface engendrée par une section plane de cylindre qui roule sur un plan.
Gd-005 Surface engendrée par une section plane de cylindre qui roule sur un plan. Gd-006 Surface engendrée par une courbe d'un cylindre qui roule sur un plan.
Gd-006 Surface engendrée par une courbe d'un cylindre qui roule sur un plan. Gd-007 Surface définie paramétriquement.
Gd-007 Surface définie paramétriquement. Gd-008 Surface définie paramétriquement.
Gd-008 Surface définie paramétriquement. Gd-009 Surface définie paramétriquement.
Gd-009 Surface définie paramétriquement. Gd-010 Surface correspondant à la sphère avec orthogonalité des éléments.
Gd-010 Surface correspondant à la sphère avec orthogonalité des éléments. Gd-011 Modèle de l'emplacement des centres des cordes d'une courbe gauche.
Gd-011 Modèle de l'emplacement des centres des cordes d'une courbe gauche. Gd-012 Modèle de l'interface du réseau parabolique de rayons.
Gd-012 Modèle de l'interface du réseau parabolique de rayons. Gd-013 Hyperboloϊde double.
Gd-013 Hyperboloϊde double. Gd-014 Modèle de la surface \( z=x\ y\ \cdot \frac{x^2-y^2}{x^2+y^2} \), pour son point zéro singulier \( \frac{\delta^2\ z}{\delta\ x\ \delta\ y}\neq \frac{\delta^2\ z}{\delta\ y\ \delta\ x} \).
Gd-014 Modèle de la surface \( z=x\ y\ \cdot \frac{x^2-y^2}{x^2+y^2} \), pour son point zéro singulier \( \frac{\delta^2\ z}{\delta\ x\ \delta\ y}\neq \frac{\delta^2\ z}{\delta\ y\ \delta\ x} \). Gd-015 Modèle d'une surface du 3ème degré, pour expliquer le comportement d'une surface courbe à proximité d'un point parabolique.
Gd-015 Modèle d'une surface du 3ème degré, pour expliquer le comportement d'une surface courbe à proximité d'un point parabolique. Gd-016 Cône sinusoïdale à trois saillies et creux, avec sections horizontales. Cette surface est engendrée par une droite qui glisse sur une courbe sinusoïdale enroulée sur un cylindre et qui passe constamment par un même point situé sur l’axe de ce cylindre.
Gd-016 Cône sinusoïdale à trois saillies et creux, avec sections horizontales. Cette surface est engendrée par une droite qui glisse sur une courbe sinusoïdale enroulée sur un cylindre et qui passe constamment par un même point situé sur l’axe de ce cylindre. Gd-017 Surface engendrée par une section plane d'un cylindre qui roule sur un cylindre.
Gd-017 Surface engendrée par une section plane d'un cylindre qui roule sur un cylindre. Gd-018 Graphe de la fonction \(z=\frac{x^2y^2}{(x^2+y^2)^{3/2}}\).
Gd-018 Graphe de la fonction \(z=\frac{x^2y^2}{(x^2+y^2)^{3/2}}\). Gd-App-001 Surface hélicoidale applicable sur l'éllipsoide de révolution, version en bois.
Gd-App-001 Surface hélicoidale applicable sur l'éllipsoide de révolution, version en bois. Gd-App-002 Surface hélicoidale applicable sur l'éllipsoide de révolution.
Gd-App-002 Surface hélicoidale applicable sur l'éllipsoide de révolution. Gd-App-003 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b).
Gd-App-003 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b). Gd-App-004 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b), version en bois.
Gd-App-004 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b), version en bois. Gd-App-005 Ellipsoïde de révolution, version en laiton flexible qui s'applique sur le modèle numéro 235 (VIII, 7c).
Gd-App-005 Ellipsoïde de révolution, version en laiton flexible qui s'applique sur le modèle numéro 235 (VIII, 7c). Gd-App-006 Modèle d'une surface développable sur le paraboloïde de révolution de 12ème ordre et 10ème classe.
Gd-App-006 Modèle d'une surface développable sur le paraboloïde de révolution de 12ème ordre et 10ème classe. Gd-App-007 Surface applicable sur le paraboloïde de révolution.
Gd-App-007 Surface applicable sur le paraboloïde de révolution. Gd-App-008 Surface sur laquelle l'ellipsoïde est représenté de manière conforme par des normales parallèles.
Gd-App-008 Surface sur laquelle l'ellipsoïde est représenté de manière conforme par des normales parallèles. Gd-Can-001 Surface canal hélicoϊdale et lignes de courbure.
Gd-Can-001 Surface canal hélicoϊdale et lignes de courbure. Gd-Can-002 Surface spirale développée de sphère.
Gd-Can-002 Surface spirale développée de sphère. Gd-Can-003 Surface spirale lieu de cercles.
Gd-Can-003 Surface spirale lieu de cercles. Gd-Can-004 Surface canal engendrée par une sphère de rayon constant.
Gd-Can-004 Surface canal engendrée par une sphère de rayon constant. Gd-Cau-001 Surface du 12ème degré. Surface caustique des rayons partant d'une ligne lumineuse après leur réflexion sur un cylindre dont l'axe touche la ligne.
Gd-Cau-001 Surface du 12ème degré. Surface caustique des rayons partant d'une ligne lumineuse après leur réflexion sur un cylindre dont l'axe touche la ligne. Gd-Cau-002 Enveloppe de normales d'un conoïde de Plϋcker.
Gd-Cau-002 Enveloppe de normales d'un conoïde de Plϋcker. Gd-Cau-003 Enveloppe de normales d'un paraboloïde.
Gd-Cau-003 Enveloppe de normales d'un paraboloïde. Gd-Cau-004 Enveloppe de normales d'un hyperboloïde.
Gd-Cau-004 Enveloppe de normales d'un hyperboloïde. Gd-Cau-005 Enveloppe de normales d'un ellipsoïde.
Gd-Cau-005 Enveloppe de normales d'un ellipsoïde. Gd-Cau-006 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=-1\)
Gd-Cau-006 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=-1\) Gd-Cau-007 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=3\)
Gd-Cau-007 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=3\) Gd-Cau-008 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=\frac{b}{3}=\frac{10}{3}\)
Gd-Cau-008 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=\frac{b}{3}=\frac{10}{3}\) Gd-Cau-009 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=5,4\)
Gd-Cau-009 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=5,4\) Gd-Cau-010 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=8\)
Gd-Cau-010 Surface normales aux droites dont 3 points, de distances mutuelles constantes, se meuvent dans 3 plans rectangulaires. \(a=16, b=10, c=0\) \(K=8\)