-
 Rotary cyclostyle
Rotary cyclostyle N°52749
-
 Rulpidon 3D - 9 couleurs
Rulpidon 3D - 9 couleurs
-
 Salle des modèles du Laboratoire de géométrie supérieure de la Faculté des sciences de l'Université de Paris en 1910.
Salle des modèles du Laboratoire de géométrie supérieure de la Faculté des sciences de l'Université de Paris en 1910.
-
 Sg-001
Sg-001 Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc.
-
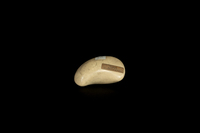 Sg-002
Sg-002 Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc.
-
 Sg-Lgc-001
Sg-Lgc-001 Surface de largeur constante.
Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton.
On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé (celui-ci), un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux.
-
 Sg-Lgc-002
Sg-Lgc-002 Surface de largeur constante.
Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton.
On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux (celui-ci).
-
 Sg-Lgc-003
Sg-Lgc-003 Surface de largeur constante.
Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton.
On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie (celui-ci), le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux .
-
 Sg-Sta-001
Sg-Sta-001 Gömböc 1928.
-
 Sg-Sta-002
Sg-Sta-002 Gömböc en plexiglass.
-
 Sophie Germain
Sophie Germain Nombre de copies : 1
Monté sur socle en bois.
Don de Alice et Roger Mansuy à l'IHP le 10/05/2021.
-
 Surface de Boy
Surface de Boy Peinture donnée par l'artiste à la bibliothèque suite à l'exposition "Patrice Jeener, le graveur de mathématiques", en 2016.
-
 Tableau D. Martet
Tableau D. Martet Oeuvre donnée par l’artiste à la bibliothèque suite à l’exposition « Promenade en mathématiques » en 2016.
-
 Tableau noir d'Émile Borel
Tableau noir d'Émile Borel Tableau exposé dès l'ouverture de la salle Pi du Palais de la découverte à Paris, en 1937.
Il s'agit d'une copie réalisée à partir d'une photo d'un tableau d'Emile Borel prise lors d'un de ses cours à l'université. Le support utilisé est un panneau de bois recouvert de peinture à tableau, sur laquelle la photo était reproduite à la peinture blanche.
À l'époque où l'éducation nationale usait de la craie, les enfants qui défilaient au Palais de la découverte avaient de la craie dans les poches et écrivaient sur le tableau de Borel. On pouvait effacer leurs bêtises sans effacer la peinture blanche reproduisant l'écriture de Borel.
-
 Tableau pliant du groupe Bourbaki
Tableau pliant du groupe Bourbaki Outil emblématique des mathématiques, le tableau noir favorise les échanges spontanés. Il permet d’écrire, de se tromper, d’effacer, de recommencer… à l’image du processus de recherche.
Les tableaux pliants permettaient au collectif de chercheurs Bourbaki de s’installer n’importe où pour travailler.
Ce tableau était conservé dans les archives de la bibliothèque de mathématiques et informatique du DMA de l'École normale supérieure. Il a été transféré à l'IHP en 2020.
-
 Timbre commémoratif de l'ICM 1998 à Berlin
Timbre commémoratif de l'ICM 1998 à Berlin Timbre réalisé par la Deutsche Post AG à l'occasion de l'International Congress of Mathematicians de 1998 à Berlin.
Motif : décomposition d'un presque carré en carrés différents les uns des autres sur fond de nombre circulaire Pi.
-
 Timbre en hommage à Sophie Germain
Timbre en hommage à Sophie Germain Timbre hommage de la Collection Historique du Timbre-Poste Français, réalisé en marge de l'exposition "Sophie Germain : 1776 - 1831" exposée à l'IHP en 2016.
-
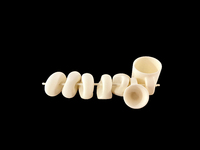 To-001
To-001 Topology joke. "La blague traditionnelle sur les topologues est qu'ils ne peuvent pas faire la différence entre une tasse à café et un donut (ou si vous préférez, un beignet)."
Surface obtenue en déformant continûment un tore : transformation de la tasse à la bouée.
-
 To-002
To-002 Topologie, le tore unilatère de Klein.
Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.
-
 To-003
To-003 Topologie : analysis situs (étude de connexions).
-
 To-004
To-004 Topologie : tore coupé.
-
 To-005
To-005 Topologie : cylindres.
-
 To-006
To-006 Topologie : morceaux de sphères.
-
 To-007
To-007 Topologie : morceaux de sphères.
-
 To-008
To-008 Topologie : morceaux de sphères.
-
 To-009
To-009 Topologie : assemblages de parallélépipèdes.
-
 To-010
To-010 Topologie : morceaux de tores.
-
 To-011
To-011 Topologie : morceaux de tores.
-
 To-012
To-012 Topologie : tore.
-
 To-013
To-013 Topologie : morceaux de sphères.
-
 To-Sno-001
To-Sno-001 Cyclide unilatère.
Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.
-
 To-Sno-002
To-Sno-002 Ruban de Möbius à bord circulaire.
-
 To-Sno-003
To-Sno-003 Bouteille de Klein en verre.
-
 To-Sno-004
To-Sno-004 Ruban de Möbius en bois.
-
 To-Sno-005
To-Sno-005 Sphère à bonnet croisé. Image du plan projectif avec 2 points pinces.
Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.
-
 To-Sno-006
To-Sno-006 Bonnet croisé. Surface du 4ème ordre avec une droite double : lieu géométrique des cercles de courbure des sections normales d'une surface quelconque dans un élément de surface à courbure positive.
-
 To-Sno-007
To-Sno-007 La surface romaine de Steiner avec des courbes de tangente principale. Elle possède trois droites doubles qui se rejoignent en un point.
-
 To-Sno-008
To-Sno-008 Modèle de la représentation du plan projectif sur une surface sans singularité fermée dans le fini.
Cette surface possède un minimum, un maximum et un maximum minimal et est ainsi la généralisation la plus simple de la sphère en ce qui concerne les extrêmes.
-
 To-Sno-009
To-Sno-009 Surface de Boy. Modèles de la représentation du plan projectif sur une surface fermée sans singularité.
Cette surface possède un axe de symétrie, de sorte que la surface coïncide avec elle-même lors d'une rotation de 120° autour de celle-ci.
-
 To-Sno-010
To-Sno-010 Ruban de Möbius coupé en deux par le milieu formant deux rubans ordinaires enlacés.
-
 To-Sno-011
To-Sno-011 Ruban de Möbius avec alphabet.
-
 To-Sno-012
To-Sno-012 Ruban de Möbius.
-
 To-Sno-013
To-Sno-013 Il s'agit d'une surface du 4ème degré possédant deux singularités du type parapluie de Withney et une ligne double qui est la droite joignant les deux singularités. Cette surface (bonnet croisé) est une image du plan projectif réel avec auto-intersection. Dans son célèbre traité sur les surfaces, Darboux évoque l'impossibilité de représenter le plan projectif dans l'espace euclidien sans auto-intersection. Sa démonstration, quoique très instructive, est incomplète car elle s'appuie sur le fait que la surface cherchée est algébrique.
-
 To-Sno-014
To-Sno-014 Surface romaine de Steiner.
-
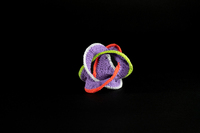 To-Sno-015
To-Sno-015 Surface non orientable bordée par des anneaux borroméens.
Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html).
-
 To-Sno-016
To-Sno-016 Ruban de Möbius (surface non orientable) bordé par un nœud de trèfle.
-
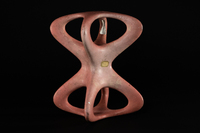 To-Sor-001
To-Sor-001 Surface de genre 6.
-
 To-Sor-002
To-Sor-002 Tore carré plat plongé isométriquement dans l'espace ambiant.
-
 To-Sor-003
To-Sor-003 Carte sur la surface de genre 2 nécessitant 8 couleurs.
-
 To-Sor-004
To-Sor-004 Surface de Morin du huitième degré.
-
 To-Sor-005
To-Sor-005 Surface de genre 3 à symétrie d'ordre 4.
-
 To-Sor-006
To-Sor-006 On trace, dans un plan vertical, une droite verticale et un cercle non centré sur la droite, puis on fait tourner le plan autour de la droite prise comme axe de révolution. Le tore est la surface décrite par le cercle. Par construction le tore contient donc une famille de cercles appelés "méridiens". Lorsque l'on coupe le tore par des plans horizontaux, on trouve une autre famille de cercles appelés "parallèles".
Il existe deux autres familles de cercles sur le tore, les "cercles d'Yvon Villarceau" nommés en hommage à leur découvreur, Antoine Yvon Villarceau. Ils sont obtenus en coupant le tore par un plan bitangent, autrement dit tangent au tore en exactement deux points distincts. On observe alors qu'un tel plan coupe le tore en deux parties égales.
Inversement, est-ce qu'un plan qui coupe le tore en deux parties égales le coupe suivant deux cercles ? La réponse est non, comme le montre ce modèle-ci, sur lequel l'intersection est une courbe de 4ème degré, car le tore lui-même est une surface du 4ème degré.
 Rotary cyclostyle N°52749
Rotary cyclostyle N°52749 Rulpidon 3D - 9 couleurs
Rulpidon 3D - 9 couleurs
 Salle des modèles du Laboratoire de géométrie supérieure de la Faculté des sciences de l'Université de Paris en 1910.
Salle des modèles du Laboratoire de géométrie supérieure de la Faculté des sciences de l'Université de Paris en 1910.
 Sg-001 Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc.
Sg-001 Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc. Sg-002 Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc.
Sg-002 Modèle en forme de haricot pour déterminer expérimentalement la courbe parabolique, les lignes de courbure et d'asymptote, etc. Sg-Lgc-001 Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé (celui-ci), un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux.
Sg-Lgc-001 Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé (celui-ci), un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux. Sg-Lgc-002 Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux (celui-ci).
Sg-Lgc-002 Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie, le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux (celui-ci). Sg-Lgc-003 Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie (celui-ci), le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux .
Sg-Lgc-003 Surface de largeur constante. Il s'agit de généralisations du triangle de Reuleaux : ces trois modèles ont le même diamètre, égal à la distance entre les deux plaques de laiton. On peut constater qu'il existe plusieurs façons de généraliser : l'un des modèles est limité par des portions de sphères centrées sur le sommet opposé, un autre est obtenu par rotation du triangle de Reuleaux autour d'un de ses axes de symétrie (celui-ci), le dernier est obtenu de la même façon à partir du second triangle de Reuleaux, sans sommet anguleux . Sg-Sta-001 Gömböc 1928.
Sg-Sta-001 Gömböc 1928. Sg-Sta-002 Gömböc en plexiglass.
Sg-Sta-002 Gömböc en plexiglass. Sophie Germain Nombre de copies : 1 Monté sur socle en bois. Don de Alice et Roger Mansuy à l'IHP le 10/05/2021.
Sophie Germain Nombre de copies : 1 Monté sur socle en bois. Don de Alice et Roger Mansuy à l'IHP le 10/05/2021. Surface de Boy Peinture donnée par l'artiste à la bibliothèque suite à l'exposition "Patrice Jeener, le graveur de mathématiques", en 2016.
Surface de Boy Peinture donnée par l'artiste à la bibliothèque suite à l'exposition "Patrice Jeener, le graveur de mathématiques", en 2016. Tableau D. Martet Oeuvre donnée par l’artiste à la bibliothèque suite à l’exposition « Promenade en mathématiques » en 2016.
Tableau D. Martet Oeuvre donnée par l’artiste à la bibliothèque suite à l’exposition « Promenade en mathématiques » en 2016. Tableau noir d'Émile Borel Tableau exposé dès l'ouverture de la salle Pi du Palais de la découverte à Paris, en 1937. Il s'agit d'une copie réalisée à partir d'une photo d'un tableau d'Emile Borel prise lors d'un de ses cours à l'université. Le support utilisé est un panneau de bois recouvert de peinture à tableau, sur laquelle la photo était reproduite à la peinture blanche. À l'époque où l'éducation nationale usait de la craie, les enfants qui défilaient au Palais de la découverte avaient de la craie dans les poches et écrivaient sur le tableau de Borel. On pouvait effacer leurs bêtises sans effacer la peinture blanche reproduisant l'écriture de Borel.
Tableau noir d'Émile Borel Tableau exposé dès l'ouverture de la salle Pi du Palais de la découverte à Paris, en 1937. Il s'agit d'une copie réalisée à partir d'une photo d'un tableau d'Emile Borel prise lors d'un de ses cours à l'université. Le support utilisé est un panneau de bois recouvert de peinture à tableau, sur laquelle la photo était reproduite à la peinture blanche. À l'époque où l'éducation nationale usait de la craie, les enfants qui défilaient au Palais de la découverte avaient de la craie dans les poches et écrivaient sur le tableau de Borel. On pouvait effacer leurs bêtises sans effacer la peinture blanche reproduisant l'écriture de Borel. Tableau pliant du groupe Bourbaki Outil emblématique des mathématiques, le tableau noir favorise les échanges spontanés. Il permet d’écrire, de se tromper, d’effacer, de recommencer… à l’image du processus de recherche. Les tableaux pliants permettaient au collectif de chercheurs Bourbaki de s’installer n’importe où pour travailler. Ce tableau était conservé dans les archives de la bibliothèque de mathématiques et informatique du DMA de l'École normale supérieure. Il a été transféré à l'IHP en 2020.
Tableau pliant du groupe Bourbaki Outil emblématique des mathématiques, le tableau noir favorise les échanges spontanés. Il permet d’écrire, de se tromper, d’effacer, de recommencer… à l’image du processus de recherche. Les tableaux pliants permettaient au collectif de chercheurs Bourbaki de s’installer n’importe où pour travailler. Ce tableau était conservé dans les archives de la bibliothèque de mathématiques et informatique du DMA de l'École normale supérieure. Il a été transféré à l'IHP en 2020. Timbre commémoratif de l'ICM 1998 à Berlin Timbre réalisé par la Deutsche Post AG à l'occasion de l'International Congress of Mathematicians de 1998 à Berlin. Motif : décomposition d'un presque carré en carrés différents les uns des autres sur fond de nombre circulaire Pi.
Timbre commémoratif de l'ICM 1998 à Berlin Timbre réalisé par la Deutsche Post AG à l'occasion de l'International Congress of Mathematicians de 1998 à Berlin. Motif : décomposition d'un presque carré en carrés différents les uns des autres sur fond de nombre circulaire Pi. Timbre en hommage à Sophie Germain Timbre hommage de la Collection Historique du Timbre-Poste Français, réalisé en marge de l'exposition "Sophie Germain : 1776 - 1831" exposée à l'IHP en 2016.
Timbre en hommage à Sophie Germain Timbre hommage de la Collection Historique du Timbre-Poste Français, réalisé en marge de l'exposition "Sophie Germain : 1776 - 1831" exposée à l'IHP en 2016. To-001 Topology joke. "La blague traditionnelle sur les topologues est qu'ils ne peuvent pas faire la différence entre une tasse à café et un donut (ou si vous préférez, un beignet)." Surface obtenue en déformant continûment un tore : transformation de la tasse à la bouée.
To-001 Topology joke. "La blague traditionnelle sur les topologues est qu'ils ne peuvent pas faire la différence entre une tasse à café et un donut (ou si vous préférez, un beignet)." Surface obtenue en déformant continûment un tore : transformation de la tasse à la bouée. To-002 Topologie, le tore unilatère de Klein. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.
To-002 Topologie, le tore unilatère de Klein. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick. To-003 Topologie : analysis situs (étude de connexions).
To-003 Topologie : analysis situs (étude de connexions). To-004 Topologie : tore coupé.
To-004 Topologie : tore coupé. To-005 Topologie : cylindres.
To-005 Topologie : cylindres. To-006 Topologie : morceaux de sphères.
To-006 Topologie : morceaux de sphères. To-007 Topologie : morceaux de sphères.
To-007 Topologie : morceaux de sphères. To-008 Topologie : morceaux de sphères.
To-008 Topologie : morceaux de sphères. To-009 Topologie : assemblages de parallélépipèdes.
To-009 Topologie : assemblages de parallélépipèdes. To-010 Topologie : morceaux de tores.
To-010 Topologie : morceaux de tores. To-011 Topologie : morceaux de tores.
To-011 Topologie : morceaux de tores. To-012 Topologie : tore.
To-012 Topologie : tore. To-013 Topologie : morceaux de sphères.
To-013 Topologie : morceaux de sphères. To-Sno-001 Cyclide unilatère. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.
To-Sno-001 Cyclide unilatère. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick. To-Sno-002 Ruban de Möbius à bord circulaire.
To-Sno-002 Ruban de Möbius à bord circulaire. To-Sno-003 Bouteille de Klein en verre.
To-Sno-003 Bouteille de Klein en verre. To-Sno-004 Ruban de Möbius en bois.
To-Sno-004 Ruban de Möbius en bois. To-Sno-005 Sphère à bonnet croisé. Image du plan projectif avec 2 points pinces. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick.
To-Sno-005 Sphère à bonnet croisé. Image du plan projectif avec 2 points pinces. Offert à Paul Belgodère (premier responsable de la bibliothèque de l'IHP) par Maurice El-Milick. To-Sno-006 Bonnet croisé. Surface du 4ème ordre avec une droite double : lieu géométrique des cercles de courbure des sections normales d'une surface quelconque dans un élément de surface à courbure positive.
To-Sno-006 Bonnet croisé. Surface du 4ème ordre avec une droite double : lieu géométrique des cercles de courbure des sections normales d'une surface quelconque dans un élément de surface à courbure positive. To-Sno-007 La surface romaine de Steiner avec des courbes de tangente principale. Elle possède trois droites doubles qui se rejoignent en un point.
To-Sno-007 La surface romaine de Steiner avec des courbes de tangente principale. Elle possède trois droites doubles qui se rejoignent en un point. To-Sno-008 Modèle de la représentation du plan projectif sur une surface sans singularité fermée dans le fini. Cette surface possède un minimum, un maximum et un maximum minimal et est ainsi la généralisation la plus simple de la sphère en ce qui concerne les extrêmes.
To-Sno-008 Modèle de la représentation du plan projectif sur une surface sans singularité fermée dans le fini. Cette surface possède un minimum, un maximum et un maximum minimal et est ainsi la généralisation la plus simple de la sphère en ce qui concerne les extrêmes. To-Sno-009 Surface de Boy. Modèles de la représentation du plan projectif sur une surface fermée sans singularité. Cette surface possède un axe de symétrie, de sorte que la surface coïncide avec elle-même lors d'une rotation de 120° autour de celle-ci.
To-Sno-009 Surface de Boy. Modèles de la représentation du plan projectif sur une surface fermée sans singularité. Cette surface possède un axe de symétrie, de sorte que la surface coïncide avec elle-même lors d'une rotation de 120° autour de celle-ci. To-Sno-010 Ruban de Möbius coupé en deux par le milieu formant deux rubans ordinaires enlacés.
To-Sno-010 Ruban de Möbius coupé en deux par le milieu formant deux rubans ordinaires enlacés. To-Sno-011 Ruban de Möbius avec alphabet.
To-Sno-011 Ruban de Möbius avec alphabet. To-Sno-012 Ruban de Möbius.
To-Sno-012 Ruban de Möbius. To-Sno-013 Il s'agit d'une surface du 4ème degré possédant deux singularités du type parapluie de Withney et une ligne double qui est la droite joignant les deux singularités. Cette surface (bonnet croisé) est une image du plan projectif réel avec auto-intersection. Dans son célèbre traité sur les surfaces, Darboux évoque l'impossibilité de représenter le plan projectif dans l'espace euclidien sans auto-intersection. Sa démonstration, quoique très instructive, est incomplète car elle s'appuie sur le fait que la surface cherchée est algébrique.
To-Sno-013 Il s'agit d'une surface du 4ème degré possédant deux singularités du type parapluie de Withney et une ligne double qui est la droite joignant les deux singularités. Cette surface (bonnet croisé) est une image du plan projectif réel avec auto-intersection. Dans son célèbre traité sur les surfaces, Darboux évoque l'impossibilité de représenter le plan projectif dans l'espace euclidien sans auto-intersection. Sa démonstration, quoique très instructive, est incomplète car elle s'appuie sur le fait que la surface cherchée est algébrique. To-Sno-014 Surface romaine de Steiner.
To-Sno-014 Surface romaine de Steiner. To-Sno-015 Surface non orientable bordée par des anneaux borroméens. Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html).
To-Sno-015 Surface non orientable bordée par des anneaux borroméens. Réalisé d’après l’atelier proposé par Shiying Dong à la conférence Bridges 2023 (https://archive.bridgesmathart.org/2023/bridges2023-559.html). To-Sno-016 Ruban de Möbius (surface non orientable) bordé par un nœud de trèfle.
To-Sno-016 Ruban de Möbius (surface non orientable) bordé par un nœud de trèfle. To-Sor-001 Surface de genre 6.
To-Sor-001 Surface de genre 6. To-Sor-002 Tore carré plat plongé isométriquement dans l'espace ambiant.
To-Sor-002 Tore carré plat plongé isométriquement dans l'espace ambiant. To-Sor-003 Carte sur la surface de genre 2 nécessitant 8 couleurs.
To-Sor-003 Carte sur la surface de genre 2 nécessitant 8 couleurs. To-Sor-004 Surface de Morin du huitième degré.
To-Sor-004 Surface de Morin du huitième degré. To-Sor-005 Surface de genre 3 à symétrie d'ordre 4.
To-Sor-005 Surface de genre 3 à symétrie d'ordre 4. To-Sor-006 On trace, dans un plan vertical, une droite verticale et un cercle non centré sur la droite, puis on fait tourner le plan autour de la droite prise comme axe de révolution. Le tore est la surface décrite par le cercle. Par construction le tore contient donc une famille de cercles appelés "méridiens". Lorsque l'on coupe le tore par des plans horizontaux, on trouve une autre famille de cercles appelés "parallèles". Il existe deux autres familles de cercles sur le tore, les "cercles d'Yvon Villarceau" nommés en hommage à leur découvreur, Antoine Yvon Villarceau. Ils sont obtenus en coupant le tore par un plan bitangent, autrement dit tangent au tore en exactement deux points distincts. On observe alors qu'un tel plan coupe le tore en deux parties égales. Inversement, est-ce qu'un plan qui coupe le tore en deux parties égales le coupe suivant deux cercles ? La réponse est non, comme le montre ce modèle-ci, sur lequel l'intersection est une courbe de 4ème degré, car le tore lui-même est une surface du 4ème degré.
To-Sor-006 On trace, dans un plan vertical, une droite verticale et un cercle non centré sur la droite, puis on fait tourner le plan autour de la droite prise comme axe de révolution. Le tore est la surface décrite par le cercle. Par construction le tore contient donc une famille de cercles appelés "méridiens". Lorsque l'on coupe le tore par des plans horizontaux, on trouve une autre famille de cercles appelés "parallèles". Il existe deux autres familles de cercles sur le tore, les "cercles d'Yvon Villarceau" nommés en hommage à leur découvreur, Antoine Yvon Villarceau. Ils sont obtenus en coupant le tore par un plan bitangent, autrement dit tangent au tore en exactement deux points distincts. On observe alors qu'un tel plan coupe le tore en deux parties égales. Inversement, est-ce qu'un plan qui coupe le tore en deux parties égales le coupe suivant deux cercles ? La réponse est non, comme le montre ce modèle-ci, sur lequel l'intersection est une courbe de 4ème degré, car le tore lui-même est une surface du 4ème degré.