-
 Gd-Rev-008
Gd-Rev-008 Surface de révolution obtenue en faisant tourner la parabole cubique autour d'une parallèle à la tangente de retournement. Équation de la surface \( z^3=a^3(r— a) \), de la projection des courbes d'asymptotes \( \varphi=\sqrt{\frac{2}{3}}\log \frac{2(r+\sqrt{r(r\pm a)})\pm a}{a} \).
-
 Gd-Rev-007
Gd-Rev-007 Surface de révolution obtenue en faisant tourner la parabole autour d'une parallèle à la tangente au sommet. Équation de la surface \( z^2= a^2(r— a) \), de la projection des courbes d'asymptotes \( \varphi=\sqrt{\frac{1}{2}}\log \frac{2(r+\sqrt{r(r-a)})-a}{a} \).
-
 Gd-Rev-006
Gd-Rev-006 Surface de révolution obtenue en faisant tourner la parabole de Neil autour de sa tangente de retour. Équation de la surface \( z^3=25\ r^2 \), de la projection des courbes d'asymptotes en coordonnées polaires \( \varphi=\sqrt{\frac{1}{3}}\log r \).
-
 Gd-Rev-005
Gd-Rev-005 Surface de révolution obtenue en faisant tourner la spirale logarithmique autour de son asymptote. Équation de la surface \( z=6\log r \), de la projection des courbes d'asymptotes \( \varphi=\log r \).
-
 Gd-Rev-004
Gd-Rev-004 Surface de révolution obtenue en faisant tourner l'hyperbole équilatérale autour d'une de ses asymptotes. Équation de la surface \( z \cdot r=6 \), de la projection des courbes d'asymptotes en coordonnées polaires \( \varphi=\sqrt{2}\log r \).
-
 Gd-Rev-003
Gd-Rev-003 Surface de révolution dont l'équation est \( zr^2=8 \). Équation des courbes d'asymptote \( \varphi=\sqrt{3}\log r \).
-
 Gd-Rev-002
Gd-Rev-002 Surface de révolution obtenue en faisant tourner la parabole cubique autour de sa tangente d'inversion. Équation de la surface \( z^3= 27r \), de la projection des courbes d'asymptotes en coordonnées polaires \( \varphi=\sqrt{\frac{2}{3}}\log r \).
-
 Gd-Rev-001
Gd-Rev-001 Surface de révolution obtenue en faisant tourner la parabole autour de sa tangente au sommet. Équation de la surface \( z^2=r\quad (r=\sqrt{x^2+y^2)} \), de la projection des courbes d'asymptotes en coordonnées polaires \( \varphi=\sqrt{\frac{1}{2}}\log r \).
-
 Gd-Reg-019
Gd-Reg-019 Surface hélicoïdale fermée inclinée, dans laquelle les génératrices vis se rencontrent de manière oblique.
-
 Gd-Reg-018
Gd-Reg-018 Hélicoϊde réglé incurvé. Pour \( \varepsilon > \sigma \) ; la section normale est une développante de cercle incurvée.
-
 Gd-Reg-017
Gd-Reg-017 Hélicoϊde réglé torsadé. Pour \( \varepsilon < \sigma \) ; la section normale est une développante de cercle torsadé.
-
 Gd-Reg-016
Gd-Reg-016 Le cylindroïde et le paraboloïde rectangulaire réunis.
Le paraboloïde rectangulaire est le lieu géométrique de tous les points qui sont équidistants de deux droites données. Il a cette position par rapport à une infinité de paires de droites, et celles-ci sont les génératrices d'un cylindroïde. Le modèle représente ces deux surfaces unies dans cette position. Les limites sont les mêmes que pour les modèles numéros 31 (XXIII, 8b) et 76 (XIII, 9b).
-
 Gd-Reg-015
Gd-Reg-015 Le cylindroïde (conoïde de Plücker).
La courbe de délimitation correspond à celle du modèle numéro 31 (XXIII, 8b). Il s'agit aussi du même fil de délimitation, mais avec des fils différemment enfilés.
-
 Gd-Reg-014
Gd-Reg-014 Le cylindroïde (conoïde de Plücker).
La courbe de délimitation correspond à celle du modèle numéro 30 (XXIII, 8a). Il s'agit aussi du même fil de délimitation, mais avec des fils différemment enfilés.
-
 Gd-Dev-001
Gd-Dev-001 Hélicoïde développable. Pour \( \varepsilon = \sigma \) ; la section normale à l'axe est une développante commune de cercle.
-
 Gd-Cau-017
Gd-Cau-017 Enveloppe des normales de l'hyperboloïde à une feuille.
Les deux manteaux réunis.
-
 Gd-Cau-016
Gd-Cau-016 Enveloppe des normales de l'hyperboloïde à une feuille.
Les deux enveloppes de la surface sont séparées, voir modèle n°121 I, 3a.
-
 Gd-Cau-015
Gd-Cau-015 Enveloppe des normales de l'hyperboloïde à une feuille.
Les deux enveloppes de la surface sont séparées, voir modèle n°122 I, 3a.
-
 Gd-Cau-014
Gd-Cau-014 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique.
Les deux enveloppes de la surface réunies (voir modèles n°118 et 119 I, 2a).
-
 Gd-Cau-013
Gd-Cau-013 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique.
Les deux enveloppes de la surface sont séparées, voir modèle n°119 I, 2a.
-
 Gd-Cau-012
Gd-Cau-012 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique.
Les deux enveloppes de la surface sont séparées, voir modèle n°118 I, 2a.
-
 Gd-Cau-001
Gd-Cau-001 Surface du 12ème degré. Surface caustique des rayons partant d'une ligne lumineuse après leur réflexion sur un cylindre dont l'axe touche la ligne.
-
 Gd-Can-001
Gd-Can-001 Surface canal hélicoϊdale et lignes de courbure.
-
 Gd-App-008
Gd-App-008 Surface sur laquelle l'ellipsoïde est représenté de manière conforme par des normales parallèles.
-
 Gd-App-006
Gd-App-006 Modèle d'une surface développable sur le paraboloïde de révolution de 12ème ordre et 10ème classe.
-
 Gd-App-005
Gd-App-005 Ellipsoïde de révolution, version en laiton flexible qui s'applique sur le modèle numéro 235 (VIII, 7c).
-
 Gd-App-004
Gd-App-004 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b), version en bois.
-
 Gd-App-003
Gd-App-003 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b).
-
 Gd-App-002
Gd-App-002 Surface hélicoidale applicable sur l'éllipsoide de révolution.
-
 Gd-App-001
Gd-App-001 Surface hélicoidale applicable sur l'éllipsoide de révolution, version en bois.
-
 Gd-015
Gd-015 Modèle d'une surface du 3ème degré, pour expliquer le comportement d'une surface courbe à proximité d'un point parabolique.
-
 Gd-014
Gd-014 Modèle de la surface \( z=x\ y\ \cdot \frac{x^2-y^2}{x^2+y^2} \), pour son point zéro singulier \( \frac{\delta^2\ z}{\delta\ x\ \delta\ y}\neq \frac{\delta^2\ z}{\delta\ y\ \delta\ x} \).
-
 Gd-012
Gd-012 Modèle de l'interface du réseau parabolique de rayons.
-
 Gd-011
Gd-011 Modèle de l'emplacement des centres des cordes d'une courbe gauche.
-
 Cy-Dup-017
Cy-Dup-017 Cyclide de Dupin.
Cyclide en anneau avec points doubles imaginaires.
-
 Cy-Dup-016
Cy-Dup-016 Cyclide de Dupin avec les courbes d'intersection de plusieurs plans en double contact.
-
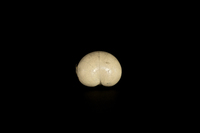 Cy-Dup-013
Cy-Dup-013 Trois types de cyclides pour lesquels les lignes de courbure sont des cercles et des courbes sphériques du 4ème ordre.
Cyclide avec 2 points doubles imaginaires combinés.
-
 Cy-Dup-010
Cy-Dup-010 Cyclide de Dupin.
Horncyclide ; deux points doubles réels unissent deux enveloppes de surface éloignées l'une de l'autre.
-
 Cy-Dup-009
Cy-Dup-009 Cyclide de Dupin.
Cyclide parabolique avec deux points doubles réels ; s'étend à l'infini avec une enveloppe de surface non appariée.
-
 Cy-Dup-008
Cy-Dup-008 Cyclide parabolique avec quatre nœuds imaginaires.
(Supplément aux cyclides de Dupin série V, n°5.)
-
 Cy-Dup-007
Cy-Dup-007 Trois types de cyclides pour lesquels les lignes de courbure sont des cercles et des courbes sphériques du 4ème ordre.
Cyclide avec 2 points doubles imaginaires combinés et un réel.
-
 Cy-Dup-006
Cy-Dup-006 Cyclide de Dupin avec les courbes d'intersection de plusieurs plans en double contact.
-
 Cy-Dup-005
Cy-Dup-005 Trois types de cyclides pour lesquels les lignes de courbure sont des cercles et des courbes sphériques du 4ème ordre.
Cyclide avec un noeud uniplanaire obtenu en contractant les 3 noeuds du n°93 (X, 8b).
-
 Cu-Reg-006
Cu-Reg-006 Surface réglée de Cayley avec points cuspidaux situés dans la partie finie.
-
 Cu-Reg-005
Cu-Reg-005 Surface réglée du 3ème degré.
L'une des droites directrices coupe le plan de l'intersection du cône directeur situé à l'infini et déterminé par un cône directeur à l'extérieur de celui-ci.
-
 Cu-Reg-003
Cu-Reg-003 Surface réglée du 3ème degré.
L'une des droites directrices coupe le plan de la section du cône directeur en dehors de la moitié de celui-ci.
-
 Cu-Poc-003
Cu-Poc-003 Aspect d'un point conique avec \( 4 \) plages convexes et indication de la courbe parabolique et des courbes tangentes à proximité du point d'origine.
-
 Cu-Poc-002
Cu-Poc-002 Aspect d'un point conique avec \( 2 \) plages convexes et indication de la courbe parabolique et des courbes tangentes à proximité du point d'origine.
-
 Cu-Poc-001
Cu-Poc-001 Aspect d'un point conique avec \( 0 \) plage convexe et indication de la courbe parabolique et des courbes tangentes à proximité du point d'origine.
-
 Cu-Dro-002
Cu-Dro-002 Surface diagonale avec 27 droites réelles.
-
 Cu-Dro-001
Cu-Dro-001 Surface du 3ème degré, 4 points singuliers. Ou cubique de Cayley.
-
 Cu-Csi-071
Cu-Csi-071 Cubique (surface du 3ème degré) avec 3 points doubles réels, auquel on ne peut pas en ajouter un 4ème.
 Gd-Rev-008 Surface de révolution obtenue en faisant tourner la parabole cubique autour d'une parallèle à la tangente de retournement. Équation de la surface \( z^3=a^3(r— a) \), de la projection des courbes d'asymptotes \( \varphi=\sqrt{\frac{2}{3}}\log \frac{2(r+\sqrt{r(r\pm a)})\pm a}{a} \).
Gd-Rev-008 Surface de révolution obtenue en faisant tourner la parabole cubique autour d'une parallèle à la tangente de retournement. Équation de la surface \( z^3=a^3(r— a) \), de la projection des courbes d'asymptotes \( \varphi=\sqrt{\frac{2}{3}}\log \frac{2(r+\sqrt{r(r\pm a)})\pm a}{a} \). Gd-Rev-007 Surface de révolution obtenue en faisant tourner la parabole autour d'une parallèle à la tangente au sommet. Équation de la surface \( z^2= a^2(r— a) \), de la projection des courbes d'asymptotes \( \varphi=\sqrt{\frac{1}{2}}\log \frac{2(r+\sqrt{r(r-a)})-a}{a} \).
Gd-Rev-007 Surface de révolution obtenue en faisant tourner la parabole autour d'une parallèle à la tangente au sommet. Équation de la surface \( z^2= a^2(r— a) \), de la projection des courbes d'asymptotes \( \varphi=\sqrt{\frac{1}{2}}\log \frac{2(r+\sqrt{r(r-a)})-a}{a} \). Gd-Rev-006 Surface de révolution obtenue en faisant tourner la parabole de Neil autour de sa tangente de retour. Équation de la surface \( z^3=25\ r^2 \), de la projection des courbes d'asymptotes en coordonnées polaires \( \varphi=\sqrt{\frac{1}{3}}\log r \).
Gd-Rev-006 Surface de révolution obtenue en faisant tourner la parabole de Neil autour de sa tangente de retour. Équation de la surface \( z^3=25\ r^2 \), de la projection des courbes d'asymptotes en coordonnées polaires \( \varphi=\sqrt{\frac{1}{3}}\log r \). Gd-Rev-005 Surface de révolution obtenue en faisant tourner la spirale logarithmique autour de son asymptote. Équation de la surface \( z=6\log r \), de la projection des courbes d'asymptotes \( \varphi=\log r \).
Gd-Rev-005 Surface de révolution obtenue en faisant tourner la spirale logarithmique autour de son asymptote. Équation de la surface \( z=6\log r \), de la projection des courbes d'asymptotes \( \varphi=\log r \). Gd-Rev-004 Surface de révolution obtenue en faisant tourner l'hyperbole équilatérale autour d'une de ses asymptotes. Équation de la surface \( z \cdot r=6 \), de la projection des courbes d'asymptotes en coordonnées polaires \( \varphi=\sqrt{2}\log r \).
Gd-Rev-004 Surface de révolution obtenue en faisant tourner l'hyperbole équilatérale autour d'une de ses asymptotes. Équation de la surface \( z \cdot r=6 \), de la projection des courbes d'asymptotes en coordonnées polaires \( \varphi=\sqrt{2}\log r \). Gd-Rev-003 Surface de révolution dont l'équation est \( zr^2=8 \). Équation des courbes d'asymptote \( \varphi=\sqrt{3}\log r \).
Gd-Rev-003 Surface de révolution dont l'équation est \( zr^2=8 \). Équation des courbes d'asymptote \( \varphi=\sqrt{3}\log r \). Gd-Rev-002 Surface de révolution obtenue en faisant tourner la parabole cubique autour de sa tangente d'inversion. Équation de la surface \( z^3= 27r \), de la projection des courbes d'asymptotes en coordonnées polaires \( \varphi=\sqrt{\frac{2}{3}}\log r \).
Gd-Rev-002 Surface de révolution obtenue en faisant tourner la parabole cubique autour de sa tangente d'inversion. Équation de la surface \( z^3= 27r \), de la projection des courbes d'asymptotes en coordonnées polaires \( \varphi=\sqrt{\frac{2}{3}}\log r \). Gd-Rev-001 Surface de révolution obtenue en faisant tourner la parabole autour de sa tangente au sommet. Équation de la surface \( z^2=r\quad (r=\sqrt{x^2+y^2)} \), de la projection des courbes d'asymptotes en coordonnées polaires \( \varphi=\sqrt{\frac{1}{2}}\log r \).
Gd-Rev-001 Surface de révolution obtenue en faisant tourner la parabole autour de sa tangente au sommet. Équation de la surface \( z^2=r\quad (r=\sqrt{x^2+y^2)} \), de la projection des courbes d'asymptotes en coordonnées polaires \( \varphi=\sqrt{\frac{1}{2}}\log r \). Gd-Reg-019 Surface hélicoïdale fermée inclinée, dans laquelle les génératrices vis se rencontrent de manière oblique.
Gd-Reg-019 Surface hélicoïdale fermée inclinée, dans laquelle les génératrices vis se rencontrent de manière oblique. Gd-Reg-018 Hélicoϊde réglé incurvé. Pour \( \varepsilon > \sigma \) ; la section normale est une développante de cercle incurvée.
Gd-Reg-018 Hélicoϊde réglé incurvé. Pour \( \varepsilon > \sigma \) ; la section normale est une développante de cercle incurvée. Gd-Reg-017 Hélicoϊde réglé torsadé. Pour \( \varepsilon < \sigma \) ; la section normale est une développante de cercle torsadé.
Gd-Reg-017 Hélicoϊde réglé torsadé. Pour \( \varepsilon < \sigma \) ; la section normale est une développante de cercle torsadé. Gd-Reg-016 Le cylindroïde et le paraboloïde rectangulaire réunis. Le paraboloïde rectangulaire est le lieu géométrique de tous les points qui sont équidistants de deux droites données. Il a cette position par rapport à une infinité de paires de droites, et celles-ci sont les génératrices d'un cylindroïde. Le modèle représente ces deux surfaces unies dans cette position. Les limites sont les mêmes que pour les modèles numéros 31 (XXIII, 8b) et 76 (XIII, 9b).
Gd-Reg-016 Le cylindroïde et le paraboloïde rectangulaire réunis. Le paraboloïde rectangulaire est le lieu géométrique de tous les points qui sont équidistants de deux droites données. Il a cette position par rapport à une infinité de paires de droites, et celles-ci sont les génératrices d'un cylindroïde. Le modèle représente ces deux surfaces unies dans cette position. Les limites sont les mêmes que pour les modèles numéros 31 (XXIII, 8b) et 76 (XIII, 9b). Gd-Reg-015 Le cylindroïde (conoïde de Plücker). La courbe de délimitation correspond à celle du modèle numéro 31 (XXIII, 8b). Il s'agit aussi du même fil de délimitation, mais avec des fils différemment enfilés.
Gd-Reg-015 Le cylindroïde (conoïde de Plücker). La courbe de délimitation correspond à celle du modèle numéro 31 (XXIII, 8b). Il s'agit aussi du même fil de délimitation, mais avec des fils différemment enfilés. Gd-Reg-014 Le cylindroïde (conoïde de Plücker). La courbe de délimitation correspond à celle du modèle numéro 30 (XXIII, 8a). Il s'agit aussi du même fil de délimitation, mais avec des fils différemment enfilés.
Gd-Reg-014 Le cylindroïde (conoïde de Plücker). La courbe de délimitation correspond à celle du modèle numéro 30 (XXIII, 8a). Il s'agit aussi du même fil de délimitation, mais avec des fils différemment enfilés. Gd-Dev-001 Hélicoïde développable. Pour \( \varepsilon = \sigma \) ; la section normale à l'axe est une développante commune de cercle.
Gd-Dev-001 Hélicoïde développable. Pour \( \varepsilon = \sigma \) ; la section normale à l'axe est une développante commune de cercle. Gd-Cau-017 Enveloppe des normales de l'hyperboloïde à une feuille. Les deux manteaux réunis.
Gd-Cau-017 Enveloppe des normales de l'hyperboloïde à une feuille. Les deux manteaux réunis. Gd-Cau-016 Enveloppe des normales de l'hyperboloïde à une feuille. Les deux enveloppes de la surface sont séparées, voir modèle n°121 I, 3a.
Gd-Cau-016 Enveloppe des normales de l'hyperboloïde à une feuille. Les deux enveloppes de la surface sont séparées, voir modèle n°121 I, 3a. Gd-Cau-015 Enveloppe des normales de l'hyperboloïde à une feuille. Les deux enveloppes de la surface sont séparées, voir modèle n°122 I, 3a.
Gd-Cau-015 Enveloppe des normales de l'hyperboloïde à une feuille. Les deux enveloppes de la surface sont séparées, voir modèle n°122 I, 3a. Gd-Cau-014 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique. Les deux enveloppes de la surface réunies (voir modèles n°118 et 119 I, 2a).
Gd-Cau-014 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique. Les deux enveloppes de la surface réunies (voir modèles n°118 et 119 I, 2a). Gd-Cau-013 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique. Les deux enveloppes de la surface sont séparées, voir modèle n°119 I, 2a.
Gd-Cau-013 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique. Les deux enveloppes de la surface sont séparées, voir modèle n°119 I, 2a. Gd-Cau-012 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique. Les deux enveloppes de la surface sont séparées, voir modèle n°118 I, 2a.
Gd-Cau-012 Enveloppe des normales d'une structure rayonnée, qui a une parenté collinéenne avec la surface du centre de courbure du paraboloïde elliptique. Les deux enveloppes de la surface sont séparées, voir modèle n°118 I, 2a. Gd-Cau-001 Surface du 12ème degré. Surface caustique des rayons partant d'une ligne lumineuse après leur réflexion sur un cylindre dont l'axe touche la ligne.
Gd-Cau-001 Surface du 12ème degré. Surface caustique des rayons partant d'une ligne lumineuse après leur réflexion sur un cylindre dont l'axe touche la ligne. Gd-Can-001 Surface canal hélicoϊdale et lignes de courbure.
Gd-Can-001 Surface canal hélicoϊdale et lignes de courbure. Gd-App-008 Surface sur laquelle l'ellipsoïde est représenté de manière conforme par des normales parallèles.
Gd-App-008 Surface sur laquelle l'ellipsoïde est représenté de manière conforme par des normales parallèles. Gd-App-006 Modèle d'une surface développable sur le paraboloïde de révolution de 12ème ordre et 10ème classe.
Gd-App-006 Modèle d'une surface développable sur le paraboloïde de révolution de 12ème ordre et 10ème classe. Gd-App-005 Ellipsoïde de révolution, version en laiton flexible qui s'applique sur le modèle numéro 235 (VIII, 7c).
Gd-App-005 Ellipsoïde de révolution, version en laiton flexible qui s'applique sur le modèle numéro 235 (VIII, 7c). Gd-App-004 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b), version en bois.
Gd-App-004 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b), version en bois. Gd-App-003 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b).
Gd-App-003 Ellipsoïde de révolution, modèle pour aller avec le modèle numéro 236 (VIII, 7b). Gd-App-002 Surface hélicoidale applicable sur l'éllipsoide de révolution.
Gd-App-002 Surface hélicoidale applicable sur l'éllipsoide de révolution. Gd-App-001 Surface hélicoidale applicable sur l'éllipsoide de révolution, version en bois.
Gd-App-001 Surface hélicoidale applicable sur l'éllipsoide de révolution, version en bois. Gd-015 Modèle d'une surface du 3ème degré, pour expliquer le comportement d'une surface courbe à proximité d'un point parabolique.
Gd-015 Modèle d'une surface du 3ème degré, pour expliquer le comportement d'une surface courbe à proximité d'un point parabolique. Gd-014 Modèle de la surface \( z=x\ y\ \cdot \frac{x^2-y^2}{x^2+y^2} \), pour son point zéro singulier \( \frac{\delta^2\ z}{\delta\ x\ \delta\ y}\neq \frac{\delta^2\ z}{\delta\ y\ \delta\ x} \).
Gd-014 Modèle de la surface \( z=x\ y\ \cdot \frac{x^2-y^2}{x^2+y^2} \), pour son point zéro singulier \( \frac{\delta^2\ z}{\delta\ x\ \delta\ y}\neq \frac{\delta^2\ z}{\delta\ y\ \delta\ x} \). Gd-012 Modèle de l'interface du réseau parabolique de rayons.
Gd-012 Modèle de l'interface du réseau parabolique de rayons. Gd-011 Modèle de l'emplacement des centres des cordes d'une courbe gauche.
Gd-011 Modèle de l'emplacement des centres des cordes d'une courbe gauche. Cy-Dup-017 Cyclide de Dupin. Cyclide en anneau avec points doubles imaginaires.
Cy-Dup-017 Cyclide de Dupin. Cyclide en anneau avec points doubles imaginaires. Cy-Dup-016 Cyclide de Dupin avec les courbes d'intersection de plusieurs plans en double contact.
Cy-Dup-016 Cyclide de Dupin avec les courbes d'intersection de plusieurs plans en double contact. Cy-Dup-013 Trois types de cyclides pour lesquels les lignes de courbure sont des cercles et des courbes sphériques du 4ème ordre. Cyclide avec 2 points doubles imaginaires combinés.
Cy-Dup-013 Trois types de cyclides pour lesquels les lignes de courbure sont des cercles et des courbes sphériques du 4ème ordre. Cyclide avec 2 points doubles imaginaires combinés. Cy-Dup-010 Cyclide de Dupin. Horncyclide ; deux points doubles réels unissent deux enveloppes de surface éloignées l'une de l'autre.
Cy-Dup-010 Cyclide de Dupin. Horncyclide ; deux points doubles réels unissent deux enveloppes de surface éloignées l'une de l'autre. Cy-Dup-009 Cyclide de Dupin. Cyclide parabolique avec deux points doubles réels ; s'étend à l'infini avec une enveloppe de surface non appariée.
Cy-Dup-009 Cyclide de Dupin. Cyclide parabolique avec deux points doubles réels ; s'étend à l'infini avec une enveloppe de surface non appariée. Cy-Dup-008 Cyclide parabolique avec quatre nœuds imaginaires. (Supplément aux cyclides de Dupin série V, n°5.)
Cy-Dup-008 Cyclide parabolique avec quatre nœuds imaginaires. (Supplément aux cyclides de Dupin série V, n°5.) Cy-Dup-007 Trois types de cyclides pour lesquels les lignes de courbure sont des cercles et des courbes sphériques du 4ème ordre. Cyclide avec 2 points doubles imaginaires combinés et un réel.
Cy-Dup-007 Trois types de cyclides pour lesquels les lignes de courbure sont des cercles et des courbes sphériques du 4ème ordre. Cyclide avec 2 points doubles imaginaires combinés et un réel. Cy-Dup-006 Cyclide de Dupin avec les courbes d'intersection de plusieurs plans en double contact.
Cy-Dup-006 Cyclide de Dupin avec les courbes d'intersection de plusieurs plans en double contact. Cy-Dup-005 Trois types de cyclides pour lesquels les lignes de courbure sont des cercles et des courbes sphériques du 4ème ordre. Cyclide avec un noeud uniplanaire obtenu en contractant les 3 noeuds du n°93 (X, 8b).
Cy-Dup-005 Trois types de cyclides pour lesquels les lignes de courbure sont des cercles et des courbes sphériques du 4ème ordre. Cyclide avec un noeud uniplanaire obtenu en contractant les 3 noeuds du n°93 (X, 8b). Cu-Reg-006 Surface réglée de Cayley avec points cuspidaux situés dans la partie finie.
Cu-Reg-006 Surface réglée de Cayley avec points cuspidaux situés dans la partie finie. Cu-Reg-005 Surface réglée du 3ème degré. L'une des droites directrices coupe le plan de l'intersection du cône directeur situé à l'infini et déterminé par un cône directeur à l'extérieur de celui-ci.
Cu-Reg-005 Surface réglée du 3ème degré. L'une des droites directrices coupe le plan de l'intersection du cône directeur situé à l'infini et déterminé par un cône directeur à l'extérieur de celui-ci. Cu-Reg-003 Surface réglée du 3ème degré. L'une des droites directrices coupe le plan de la section du cône directeur en dehors de la moitié de celui-ci.
Cu-Reg-003 Surface réglée du 3ème degré. L'une des droites directrices coupe le plan de la section du cône directeur en dehors de la moitié de celui-ci. Cu-Poc-003 Aspect d'un point conique avec \( 4 \) plages convexes et indication de la courbe parabolique et des courbes tangentes à proximité du point d'origine.
Cu-Poc-003 Aspect d'un point conique avec \( 4 \) plages convexes et indication de la courbe parabolique et des courbes tangentes à proximité du point d'origine. Cu-Poc-002 Aspect d'un point conique avec \( 2 \) plages convexes et indication de la courbe parabolique et des courbes tangentes à proximité du point d'origine.
Cu-Poc-002 Aspect d'un point conique avec \( 2 \) plages convexes et indication de la courbe parabolique et des courbes tangentes à proximité du point d'origine. Cu-Poc-001 Aspect d'un point conique avec \( 0 \) plage convexe et indication de la courbe parabolique et des courbes tangentes à proximité du point d'origine.
Cu-Poc-001 Aspect d'un point conique avec \( 0 \) plage convexe et indication de la courbe parabolique et des courbes tangentes à proximité du point d'origine. Cu-Dro-002 Surface diagonale avec 27 droites réelles.
Cu-Dro-002 Surface diagonale avec 27 droites réelles. Cu-Dro-001 Surface du 3ème degré, 4 points singuliers. Ou cubique de Cayley.
Cu-Dro-001 Surface du 3ème degré, 4 points singuliers. Ou cubique de Cayley. Cu-Csi-071 Cubique (surface du 3ème degré) avec 3 points doubles réels, auquel on ne peut pas en ajouter un 4ème.
Cu-Csi-071 Cubique (surface du 3ème degré) avec 3 points doubles réels, auquel on ne peut pas en ajouter un 4ème.