-
 Hammond n°12
Hammond n°12 N°113239
-
 Henri Becquerel
Henri Becquerel Inscription recto :
"Henri Becquerel
1852-1908
A. Guzman"
-
 Henri Poincaré
Henri Poincaré Prix du roi de Suède Oscar II à Henri Poincaré 1889. Henri Poincaré fut le lauréat du concours organisé par le roi de Suéde sur la stabilité du système solaire.
-
 Henri Poincaré
Henri Poincaré Inscription recto :
"1854-1912
Henri Poincaré Membre de l'Académie Française et de l'Académie des Sciences"
-
 Henri Poincaré
Henri Poincaré Inscription recto :
"Henri Poincaré
1854-1912
Membre de l'Académie Française et de l'Académie des Sciences
Corbin"
-
 Henri Poincaré
Henri Poincaré L'institut conserve un dessin préparatoire à cette médaille.
---
-
 Henri Poincaré - Centenaire
Henri Poincaré - Centenaire Médaille du centenaire de la disparition d'Henri Poincaré, évènement organisé par l'Institut Henri Poincaré et l'École polytechnique tout au long de l'année 2012.
Le revers a été pensé avec Cédric Villani qui le commente ainsi : « La médaille est construite autour d’une hyper sphère et de trois corps en interaction gravitationnelle. Le problème des trois corps a, en effet, valu une célébrité considérable à Poincaré lorsqu’il a reçu en 1889 la médaille d’or offerte par Oscar II, roi de Suède et de Norvège, pour la résolution de ce problème mis à concours. À dire vrai, la solution de Poincaré était finalement erronée et a été magistralement corrigée par Poincaré lui-même ; les instabilités qu’il mit au jour à cette occasion ont été plus tard développées pour donner naissance à la théorie du chaos, évoquée dans l’ellipse de gauche, dans laquelle sont représentées des variations chaotiques des trajectoires des planètes du système solaire et l’emblématique attracteur de Lorenz. Dans l’ellipse de droite figure un pavage aléatoire évoquant l’intérêt de Poincaré pour les théories probabilistes. Au centre, un bitore et un flot de Ricci célèbrent la création de la topologie par Poincaré et la solution, cent ans après son énonciation, de la fameuse conjecture qui porte son nom. Enfin en partie inférieure, on trouve des polygones curvilignes des fonctions kleiniennes que Poincaré, dans un éclair d’intuition resté fameux, rapprocha de certains modèles de géométrie non euclidienne. »
---
-
 Henri Poincaré - Moule recto
Henri Poincaré - Moule recto Moule pour le recto de la médaille commémorative du centenaire de la disparition d'Henri Poincaré.
---
-
 Henri Poincaré - Moule verso
Henri Poincaré - Moule verso Moule pour le verso de la médaille commémorative du centenaire de la disparition d'Henri Poincaré.
---
-
 Holomètre
Holomètre "Holomètre ou Echelle générale de proportions pour les applications de la
Geometrie aux arts du Dessin et spécialement pour toutes les opérations de
la Perspective Linéaire."
-
 Hommage à Maurice Audin
Hommage à Maurice Audin Inscription :
"الجمهورية الجزائرية الديمقراطية الشعبية
وزارة التعليم العالي والبحث العلمي
En hommage à Maurice Audin
Alger le 10 décembre 2018"
-
 Hommage de la ville de Saint-Affrique
Hommage de la ville de Saint-Affrique Inscription verso :
"Hommage de la ville de Saint-Affrique
Institut Henri Poincaré
6-8 septembre 2022"
-
 Institut Henri Poincaré
Institut Henri Poincaré Inscription recto :
"Institut Henri Poincaré
2010 C. Gondard"
-
 Intégraphe à plateau
Intégraphe à plateau Les intégraphes tracent une courbe, dite courbe intégrale, qui, à chaque instant, définit la valeur de l’intégrale à calculer, tout en permettant de suivre les variations de l’intégration.
Dans ces appareils, une roulette à profil aigu est maintenue suffisamment pressée sur une surface d’appui. Elle se déplacera ainsi toujours dans la direction de son plan dont l’orientation est constamment parallèle à une droite appelée directrice de l’intégration et dont le coefficient angulaire reste dans un rapport constant avec les longueurs d’ordonnées de la courbe à intégrer.
Cet intégraphe à plateau est particulièrement intéressant à utiliser pour l’intégration de petites figures. La roulette intégrante de cet instrument n’a pas de mouvements de translation ; elle s’oriente simplement et c’est la table d’appui qui se déplace.
(Catalogue d'orientation n°37 G. Coradi, s.d.)
-
 Jean Favard
Jean Favard Inscription recto :
"Jean Favard
A.H. Torcheux"
-
 Jean Perrin
Jean Perrin Inscription verso :
"1870-1942
Jean Perrin
Luzanowsky"
-
 Jean Verne
Jean Verne Inscription recto :
"Professeur Jean Verne secrétaire général de l'A.F.A.S.
Muller"
-
 Jeu d'empilement #1
Jeu d'empilement #1 Plateau de jeu d'empilement.
-
 Jeu d'empilement #2
Jeu d'empilement #2 Plateau de jeu d'empilement.
-
 Joseph Pérés
Joseph Pérés Inscription recto :
"Joseph Pérés
1890-1962
H. Dropsy"
-
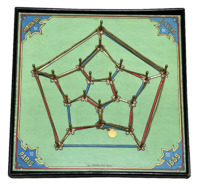 L'Icosagonal - Jeux des 20 forts
L'Icosagonal - Jeux des 20 forts Fait partie d'une série des 6 jeux scientifiques conçue par Édouard Lucas, éditée par Chambon & Baye, et présentée à l'exposition universelle de Paris 1889.
Le plateau de jeu de l'Icosagonal représente 30 arêtes colorées en bleu, blanc et rouge. La chaîne permet de tracer un chemin en suivant les arêtes et en passant par les forts.
Nouveaux jeux de combinaisons, à savoir : La Ronde du Gros Major – Le Terminus-Hôtel – L’impasse Vide Gousset – La Quarantaine – Solo de Pentagone – Grand duo sur le dos des K-èdres.
-
 Le promeneur de mathématiques
Le promeneur de mathématiques Oeuvre donnée par l’artiste à la bibliothèque suite à l’exposition « Promenade en mathématiques » en 2016.
-
 Liquid #1
Liquid #1 Donné à l'IHP par Dan Betea en 2017 dans le cadre du trimestre de recherche "Combinatorics and interactions" organisé par le Centre Émile Borel.
-
 MADAS
MADAS N°40137
Modèle VIIe TA TOMIS
-
 Maquette de la salle Pi
Maquette de la salle Pi Maquette à toucher échelle 1/30 de la salle Pi du Palais de la découverte, fondé en 1937 par Jean Perrin. Sa fonctionnalité était de permettre au public malvoyant présent physiquement dans la salle de se la représenter grâce au braille présent sur la maquette.
La salle Pi, dédiée aux mathématiques était présente dès 1937. On y trouvait les 707 premières décimales du célèbre nombre π (« pi ») telles que publiées en 1874 par William Shanks, qui avait passé 20 de sa vie à les calculer… à la main !
En 1946, Ferguson met en évidence une erreur : les décimales de Shanks sont fausses à partir de la 528ème. Les décimales de π seront corrigées plus tard, grâce au calcul par ordinateur. Aujourd’hui, on sait en calculer plusieurs milliers de milliards – et le record ne cesse d’être battu !
-
 Michel Chasles
Michel Chasles Inscription verso :
"Géomètre français
1793-1880
C. Santoni"
-
 Millionnaire
Millionnaire N°1317
Modèle X ou 10SMH
-
 Montre logarithmique
Montre logarithmique Règle à calculer circulaire.
Disque unique, gradué sur une face seulement. Aiguilles à ouverture réglable. Pivot amovible et recentrable d'après repères absolus.
Ses 3 échelles superposées (une trigonométrique, 360 degrés, une logarithmique débutant avec 4 décimales, une arithmétique pointée de 1 à 1000) résolvent tous les calculs résolus sur règle, à savoir :
Produits, quotients, puissances, racines, inverses, rapports multiples et sous-multiples des nombres. Leurs logarithmes. Addition et soustraction simples. Degrés convertis en grades. Leurs longueurs d'arc.
Ses deux axes de coordonnées, divisés en 10 à partir du centre, produisent, en grandeur et en signe, les sinus et cosinus de ses 360°.
Elle sert de rapporteur. Ses deux aiguilles, considérées comme alidades, en font un goniomètre. Les carrés et les cubes des nombres une fois formés, s'y lisent avec plus de décimales que sur les règles existantes.
-
 Nestler's Rechenwalze
Nestler's Rechenwalze Rouleau de calcul Nestler modèle n°45, équivalent d'une règle à calcul de 12,5 mètre de long.
-
 Od-001
Od-001 Surface de Gauss.
-
 Od-002
Od-002 Surface de Gauss.
-
 Od-003
Od-003 Surface statistique en plâtre indiquant la corrélation qui existe dans la distribution des atouts entre deux mains au jeu du Whist.
-
 Od-004
Od-004 Surface empirique de Galton, indiquant la corrélation qui existe entre la taille des pères et celles de leurs fils.
-
 Od-005
Od-005 Surfaces diverses remarquables.
-
 Od-006
Od-006 Projection d’un cercle dans diverses positions
-
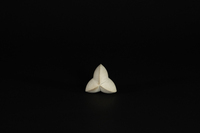 Od-007
Od-007 Surface du 4ème ordre.
-
 Od-008
Od-008 Lot de 7 pièces en plâtre.
-
 Od-009
Od-009 Surface du 4ème ordre.
-
 Od-010
Od-010 Surface statistique représentant la variation de la mortalité aux différents âges, en Suède, de 1830 à 1920
-
 Parabolographe
Parabolographe Le parabolographe permet de développer instantanément n’importe quelle parabole située dans son rayon d’action d’après les seules données suivantes : l’axe de la parabole, la tangente au sommet de la parabole, un point quelconque situé sur la parabole.
Il est le premier instrument qui a été construit pour tracer graphiquement, avec une grande précision et rapidité, des paraboles, dans des conditions répondant aux besoins réels du travail courant dans les bureaux.
(Manuel parabolographe G. Coradi, 1935)
-
 Parcours du cavalier
Parcours du cavalier Problème : peut-on parcourir toutes les cases d'un échiquier en effectuant des sauts de cavalier ?
Dans ce montage dû à Édouard Lucas, les 64 cases sont matérialisées par les tiges, et le trajet du cavalier par les chaines brisées.
La solution présentée ici est due à Euler et fournit un trajet fermé.
-
 Paul Malliavin
Paul Malliavin Inscription recto :
"Paul Malliavin
1925-2010
Membre de l'Académie des sciences
C. Gondard"
-
 Pavés Florentin du père Sébastien
Pavés Florentin du père Sébastien Fait partie d'une série des 6 jeux scientifiques conçue par Édouard Lucas, éditée par Chambon & Baye, et présentée à l'exposition universelle de Paris 1889.
Le plateau composé de pavés mi-partis permet la diffusion d'un savoir mathématique lié aux combinaisons. Ces pavés sont des carrés du plan divisés par une diagonale en deux parties de couleur différente.
-
 Photo de l'ICM 1954
Photo de l'ICM 1954 Photographie de tous les participants et participantes assemblés lors de l'ICM (International Congress of Mathematicians) de 1954 à Amsterdam.
-
 Photographie T. Chotteau #1
Photographie T. Chotteau #1 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP.
-
 Photographie T. Chotteau #2
Photographie T. Chotteau #2 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP.
-
 Photographie T. Chotteau #3
Photographie T. Chotteau #3 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP.
-
 PJ-L-001
PJ-L-001 Surface minimale à la courbe de poursuite.
-
 PJ-L-002
PJ-L-002 Écorché de la surface de Boy.
-
 PJ-L-003
PJ-L-003 Fonctions de Weierstrass.
-
 PJ-L-004
PJ-L-004
-
 PJ-L-005
PJ-L-005 Fractal cubique.
 Hammond n°12 N°113239
Hammond n°12 N°113239 Henri Becquerel Inscription recto : "Henri Becquerel 1852-1908 A. Guzman"
Henri Becquerel Inscription recto : "Henri Becquerel 1852-1908 A. Guzman" Henri Poincaré Prix du roi de Suède Oscar II à Henri Poincaré 1889. Henri Poincaré fut le lauréat du concours organisé par le roi de Suéde sur la stabilité du système solaire.
Henri Poincaré Prix du roi de Suède Oscar II à Henri Poincaré 1889. Henri Poincaré fut le lauréat du concours organisé par le roi de Suéde sur la stabilité du système solaire. Henri Poincaré Inscription recto : "1854-1912 Henri Poincaré Membre de l'Académie Française et de l'Académie des Sciences"
Henri Poincaré Inscription recto : "1854-1912 Henri Poincaré Membre de l'Académie Française et de l'Académie des Sciences" Henri Poincaré Inscription recto : "Henri Poincaré 1854-1912 Membre de l'Académie Française et de l'Académie des Sciences Corbin"
Henri Poincaré Inscription recto : "Henri Poincaré 1854-1912 Membre de l'Académie Française et de l'Académie des Sciences Corbin" Henri Poincaré L'institut conserve un dessin préparatoire à cette médaille. ---
Henri Poincaré L'institut conserve un dessin préparatoire à cette médaille. --- Henri Poincaré - Centenaire Médaille du centenaire de la disparition d'Henri Poincaré, évènement organisé par l'Institut Henri Poincaré et l'École polytechnique tout au long de l'année 2012. Le revers a été pensé avec Cédric Villani qui le commente ainsi : « La médaille est construite autour d’une hyper sphère et de trois corps en interaction gravitationnelle. Le problème des trois corps a, en effet, valu une célébrité considérable à Poincaré lorsqu’il a reçu en 1889 la médaille d’or offerte par Oscar II, roi de Suède et de Norvège, pour la résolution de ce problème mis à concours. À dire vrai, la solution de Poincaré était finalement erronée et a été magistralement corrigée par Poincaré lui-même ; les instabilités qu’il mit au jour à cette occasion ont été plus tard développées pour donner naissance à la théorie du chaos, évoquée dans l’ellipse de gauche, dans laquelle sont représentées des variations chaotiques des trajectoires des planètes du système solaire et l’emblématique attracteur de Lorenz. Dans l’ellipse de droite figure un pavage aléatoire évoquant l’intérêt de Poincaré pour les théories probabilistes. Au centre, un bitore et un flot de Ricci célèbrent la création de la topologie par Poincaré et la solution, cent ans après son énonciation, de la fameuse conjecture qui porte son nom. Enfin en partie inférieure, on trouve des polygones curvilignes des fonctions kleiniennes que Poincaré, dans un éclair d’intuition resté fameux, rapprocha de certains modèles de géométrie non euclidienne. » ---
Henri Poincaré - Centenaire Médaille du centenaire de la disparition d'Henri Poincaré, évènement organisé par l'Institut Henri Poincaré et l'École polytechnique tout au long de l'année 2012. Le revers a été pensé avec Cédric Villani qui le commente ainsi : « La médaille est construite autour d’une hyper sphère et de trois corps en interaction gravitationnelle. Le problème des trois corps a, en effet, valu une célébrité considérable à Poincaré lorsqu’il a reçu en 1889 la médaille d’or offerte par Oscar II, roi de Suède et de Norvège, pour la résolution de ce problème mis à concours. À dire vrai, la solution de Poincaré était finalement erronée et a été magistralement corrigée par Poincaré lui-même ; les instabilités qu’il mit au jour à cette occasion ont été plus tard développées pour donner naissance à la théorie du chaos, évoquée dans l’ellipse de gauche, dans laquelle sont représentées des variations chaotiques des trajectoires des planètes du système solaire et l’emblématique attracteur de Lorenz. Dans l’ellipse de droite figure un pavage aléatoire évoquant l’intérêt de Poincaré pour les théories probabilistes. Au centre, un bitore et un flot de Ricci célèbrent la création de la topologie par Poincaré et la solution, cent ans après son énonciation, de la fameuse conjecture qui porte son nom. Enfin en partie inférieure, on trouve des polygones curvilignes des fonctions kleiniennes que Poincaré, dans un éclair d’intuition resté fameux, rapprocha de certains modèles de géométrie non euclidienne. » --- Henri Poincaré - Moule recto Moule pour le recto de la médaille commémorative du centenaire de la disparition d'Henri Poincaré. ---
Henri Poincaré - Moule recto Moule pour le recto de la médaille commémorative du centenaire de la disparition d'Henri Poincaré. --- Henri Poincaré - Moule verso Moule pour le verso de la médaille commémorative du centenaire de la disparition d'Henri Poincaré. ---
Henri Poincaré - Moule verso Moule pour le verso de la médaille commémorative du centenaire de la disparition d'Henri Poincaré. --- Holomètre "Holomètre ou Echelle générale de proportions pour les applications de la Geometrie aux arts du Dessin et spécialement pour toutes les opérations de la Perspective Linéaire."
Holomètre "Holomètre ou Echelle générale de proportions pour les applications de la Geometrie aux arts du Dessin et spécialement pour toutes les opérations de la Perspective Linéaire." Hommage à Maurice Audin Inscription : "الجمهورية الجزائرية الديمقراطية الشعبية وزارة التعليم العالي والبحث العلمي En hommage à Maurice Audin Alger le 10 décembre 2018"
Hommage à Maurice Audin Inscription : "الجمهورية الجزائرية الديمقراطية الشعبية وزارة التعليم العالي والبحث العلمي En hommage à Maurice Audin Alger le 10 décembre 2018" Hommage de la ville de Saint-Affrique Inscription verso : "Hommage de la ville de Saint-Affrique Institut Henri Poincaré 6-8 septembre 2022"
Hommage de la ville de Saint-Affrique Inscription verso : "Hommage de la ville de Saint-Affrique Institut Henri Poincaré 6-8 septembre 2022" Institut Henri Poincaré Inscription recto : "Institut Henri Poincaré 2010 C. Gondard"
Institut Henri Poincaré Inscription recto : "Institut Henri Poincaré 2010 C. Gondard" Intégraphe à plateau Les intégraphes tracent une courbe, dite courbe intégrale, qui, à chaque instant, définit la valeur de l’intégrale à calculer, tout en permettant de suivre les variations de l’intégration. Dans ces appareils, une roulette à profil aigu est maintenue suffisamment pressée sur une surface d’appui. Elle se déplacera ainsi toujours dans la direction de son plan dont l’orientation est constamment parallèle à une droite appelée directrice de l’intégration et dont le coefficient angulaire reste dans un rapport constant avec les longueurs d’ordonnées de la courbe à intégrer. Cet intégraphe à plateau est particulièrement intéressant à utiliser pour l’intégration de petites figures. La roulette intégrante de cet instrument n’a pas de mouvements de translation ; elle s’oriente simplement et c’est la table d’appui qui se déplace. (Catalogue d'orientation n°37 G. Coradi, s.d.)
Intégraphe à plateau Les intégraphes tracent une courbe, dite courbe intégrale, qui, à chaque instant, définit la valeur de l’intégrale à calculer, tout en permettant de suivre les variations de l’intégration. Dans ces appareils, une roulette à profil aigu est maintenue suffisamment pressée sur une surface d’appui. Elle se déplacera ainsi toujours dans la direction de son plan dont l’orientation est constamment parallèle à une droite appelée directrice de l’intégration et dont le coefficient angulaire reste dans un rapport constant avec les longueurs d’ordonnées de la courbe à intégrer. Cet intégraphe à plateau est particulièrement intéressant à utiliser pour l’intégration de petites figures. La roulette intégrante de cet instrument n’a pas de mouvements de translation ; elle s’oriente simplement et c’est la table d’appui qui se déplace. (Catalogue d'orientation n°37 G. Coradi, s.d.) Jean Favard Inscription recto : "Jean Favard A.H. Torcheux"
Jean Favard Inscription recto : "Jean Favard A.H. Torcheux" Jean Perrin Inscription verso : "1870-1942 Jean Perrin Luzanowsky"
Jean Perrin Inscription verso : "1870-1942 Jean Perrin Luzanowsky" Jean Verne Inscription recto : "Professeur Jean Verne secrétaire général de l'A.F.A.S. Muller"
Jean Verne Inscription recto : "Professeur Jean Verne secrétaire général de l'A.F.A.S. Muller" Jeu d'empilement #1 Plateau de jeu d'empilement.
Jeu d'empilement #1 Plateau de jeu d'empilement. Jeu d'empilement #2 Plateau de jeu d'empilement.
Jeu d'empilement #2 Plateau de jeu d'empilement. Joseph Pérés Inscription recto : "Joseph Pérés 1890-1962 H. Dropsy"
Joseph Pérés Inscription recto : "Joseph Pérés 1890-1962 H. Dropsy" L'Icosagonal - Jeux des 20 forts Fait partie d'une série des 6 jeux scientifiques conçue par Édouard Lucas, éditée par Chambon & Baye, et présentée à l'exposition universelle de Paris 1889. Le plateau de jeu de l'Icosagonal représente 30 arêtes colorées en bleu, blanc et rouge. La chaîne permet de tracer un chemin en suivant les arêtes et en passant par les forts. Nouveaux jeux de combinaisons, à savoir : La Ronde du Gros Major – Le Terminus-Hôtel – L’impasse Vide Gousset – La Quarantaine – Solo de Pentagone – Grand duo sur le dos des K-èdres.
L'Icosagonal - Jeux des 20 forts Fait partie d'une série des 6 jeux scientifiques conçue par Édouard Lucas, éditée par Chambon & Baye, et présentée à l'exposition universelle de Paris 1889. Le plateau de jeu de l'Icosagonal représente 30 arêtes colorées en bleu, blanc et rouge. La chaîne permet de tracer un chemin en suivant les arêtes et en passant par les forts. Nouveaux jeux de combinaisons, à savoir : La Ronde du Gros Major – Le Terminus-Hôtel – L’impasse Vide Gousset – La Quarantaine – Solo de Pentagone – Grand duo sur le dos des K-èdres. Le promeneur de mathématiques Oeuvre donnée par l’artiste à la bibliothèque suite à l’exposition « Promenade en mathématiques » en 2016.
Le promeneur de mathématiques Oeuvre donnée par l’artiste à la bibliothèque suite à l’exposition « Promenade en mathématiques » en 2016. Liquid #1 Donné à l'IHP par Dan Betea en 2017 dans le cadre du trimestre de recherche "Combinatorics and interactions" organisé par le Centre Émile Borel.
Liquid #1 Donné à l'IHP par Dan Betea en 2017 dans le cadre du trimestre de recherche "Combinatorics and interactions" organisé par le Centre Émile Borel. MADAS N°40137 Modèle VIIe TA TOMIS
MADAS N°40137 Modèle VIIe TA TOMIS Maquette de la salle Pi Maquette à toucher échelle 1/30 de la salle Pi du Palais de la découverte, fondé en 1937 par Jean Perrin. Sa fonctionnalité était de permettre au public malvoyant présent physiquement dans la salle de se la représenter grâce au braille présent sur la maquette. La salle Pi, dédiée aux mathématiques était présente dès 1937. On y trouvait les 707 premières décimales du célèbre nombre π (« pi ») telles que publiées en 1874 par William Shanks, qui avait passé 20 de sa vie à les calculer… à la main ! En 1946, Ferguson met en évidence une erreur : les décimales de Shanks sont fausses à partir de la 528ème. Les décimales de π seront corrigées plus tard, grâce au calcul par ordinateur. Aujourd’hui, on sait en calculer plusieurs milliers de milliards – et le record ne cesse d’être battu !
Maquette de la salle Pi Maquette à toucher échelle 1/30 de la salle Pi du Palais de la découverte, fondé en 1937 par Jean Perrin. Sa fonctionnalité était de permettre au public malvoyant présent physiquement dans la salle de se la représenter grâce au braille présent sur la maquette. La salle Pi, dédiée aux mathématiques était présente dès 1937. On y trouvait les 707 premières décimales du célèbre nombre π (« pi ») telles que publiées en 1874 par William Shanks, qui avait passé 20 de sa vie à les calculer… à la main ! En 1946, Ferguson met en évidence une erreur : les décimales de Shanks sont fausses à partir de la 528ème. Les décimales de π seront corrigées plus tard, grâce au calcul par ordinateur. Aujourd’hui, on sait en calculer plusieurs milliers de milliards – et le record ne cesse d’être battu ! Michel Chasles Inscription verso : "Géomètre français 1793-1880 C. Santoni"
Michel Chasles Inscription verso : "Géomètre français 1793-1880 C. Santoni" Millionnaire N°1317 Modèle X ou 10SMH
Millionnaire N°1317 Modèle X ou 10SMH Montre logarithmique Règle à calculer circulaire. Disque unique, gradué sur une face seulement. Aiguilles à ouverture réglable. Pivot amovible et recentrable d'après repères absolus. Ses 3 échelles superposées (une trigonométrique, 360 degrés, une logarithmique débutant avec 4 décimales, une arithmétique pointée de 1 à 1000) résolvent tous les calculs résolus sur règle, à savoir : Produits, quotients, puissances, racines, inverses, rapports multiples et sous-multiples des nombres. Leurs logarithmes. Addition et soustraction simples. Degrés convertis en grades. Leurs longueurs d'arc. Ses deux axes de coordonnées, divisés en 10 à partir du centre, produisent, en grandeur et en signe, les sinus et cosinus de ses 360°. Elle sert de rapporteur. Ses deux aiguilles, considérées comme alidades, en font un goniomètre. Les carrés et les cubes des nombres une fois formés, s'y lisent avec plus de décimales que sur les règles existantes.
Montre logarithmique Règle à calculer circulaire. Disque unique, gradué sur une face seulement. Aiguilles à ouverture réglable. Pivot amovible et recentrable d'après repères absolus. Ses 3 échelles superposées (une trigonométrique, 360 degrés, une logarithmique débutant avec 4 décimales, une arithmétique pointée de 1 à 1000) résolvent tous les calculs résolus sur règle, à savoir : Produits, quotients, puissances, racines, inverses, rapports multiples et sous-multiples des nombres. Leurs logarithmes. Addition et soustraction simples. Degrés convertis en grades. Leurs longueurs d'arc. Ses deux axes de coordonnées, divisés en 10 à partir du centre, produisent, en grandeur et en signe, les sinus et cosinus de ses 360°. Elle sert de rapporteur. Ses deux aiguilles, considérées comme alidades, en font un goniomètre. Les carrés et les cubes des nombres une fois formés, s'y lisent avec plus de décimales que sur les règles existantes. Nestler's Rechenwalze Rouleau de calcul Nestler modèle n°45, équivalent d'une règle à calcul de 12,5 mètre de long.
Nestler's Rechenwalze Rouleau de calcul Nestler modèle n°45, équivalent d'une règle à calcul de 12,5 mètre de long. Od-001 Surface de Gauss.
Od-001 Surface de Gauss. Od-002 Surface de Gauss.
Od-002 Surface de Gauss. Od-003 Surface statistique en plâtre indiquant la corrélation qui existe dans la distribution des atouts entre deux mains au jeu du Whist.
Od-003 Surface statistique en plâtre indiquant la corrélation qui existe dans la distribution des atouts entre deux mains au jeu du Whist. Od-004 Surface empirique de Galton, indiquant la corrélation qui existe entre la taille des pères et celles de leurs fils.
Od-004 Surface empirique de Galton, indiquant la corrélation qui existe entre la taille des pères et celles de leurs fils. Od-005 Surfaces diverses remarquables.
Od-005 Surfaces diverses remarquables. Od-006 Projection d’un cercle dans diverses positions
Od-006 Projection d’un cercle dans diverses positions Od-007 Surface du 4ème ordre.
Od-007 Surface du 4ème ordre. Od-008 Lot de 7 pièces en plâtre.
Od-008 Lot de 7 pièces en plâtre. Od-009 Surface du 4ème ordre.
Od-009 Surface du 4ème ordre. Od-010 Surface statistique représentant la variation de la mortalité aux différents âges, en Suède, de 1830 à 1920
Od-010 Surface statistique représentant la variation de la mortalité aux différents âges, en Suède, de 1830 à 1920 Parabolographe Le parabolographe permet de développer instantanément n’importe quelle parabole située dans son rayon d’action d’après les seules données suivantes : l’axe de la parabole, la tangente au sommet de la parabole, un point quelconque situé sur la parabole. Il est le premier instrument qui a été construit pour tracer graphiquement, avec une grande précision et rapidité, des paraboles, dans des conditions répondant aux besoins réels du travail courant dans les bureaux. (Manuel parabolographe G. Coradi, 1935)
Parabolographe Le parabolographe permet de développer instantanément n’importe quelle parabole située dans son rayon d’action d’après les seules données suivantes : l’axe de la parabole, la tangente au sommet de la parabole, un point quelconque situé sur la parabole. Il est le premier instrument qui a été construit pour tracer graphiquement, avec une grande précision et rapidité, des paraboles, dans des conditions répondant aux besoins réels du travail courant dans les bureaux. (Manuel parabolographe G. Coradi, 1935) Parcours du cavalier Problème : peut-on parcourir toutes les cases d'un échiquier en effectuant des sauts de cavalier ? Dans ce montage dû à Édouard Lucas, les 64 cases sont matérialisées par les tiges, et le trajet du cavalier par les chaines brisées. La solution présentée ici est due à Euler et fournit un trajet fermé.
Parcours du cavalier Problème : peut-on parcourir toutes les cases d'un échiquier en effectuant des sauts de cavalier ? Dans ce montage dû à Édouard Lucas, les 64 cases sont matérialisées par les tiges, et le trajet du cavalier par les chaines brisées. La solution présentée ici est due à Euler et fournit un trajet fermé. Paul Malliavin Inscription recto : "Paul Malliavin 1925-2010 Membre de l'Académie des sciences C. Gondard"
Paul Malliavin Inscription recto : "Paul Malliavin 1925-2010 Membre de l'Académie des sciences C. Gondard" Pavés Florentin du père Sébastien Fait partie d'une série des 6 jeux scientifiques conçue par Édouard Lucas, éditée par Chambon & Baye, et présentée à l'exposition universelle de Paris 1889. Le plateau composé de pavés mi-partis permet la diffusion d'un savoir mathématique lié aux combinaisons. Ces pavés sont des carrés du plan divisés par une diagonale en deux parties de couleur différente.
Pavés Florentin du père Sébastien Fait partie d'une série des 6 jeux scientifiques conçue par Édouard Lucas, éditée par Chambon & Baye, et présentée à l'exposition universelle de Paris 1889. Le plateau composé de pavés mi-partis permet la diffusion d'un savoir mathématique lié aux combinaisons. Ces pavés sont des carrés du plan divisés par une diagonale en deux parties de couleur différente. Photo de l'ICM 1954 Photographie de tous les participants et participantes assemblés lors de l'ICM (International Congress of Mathematicians) de 1954 à Amsterdam.
Photo de l'ICM 1954 Photographie de tous les participants et participantes assemblés lors de l'ICM (International Congress of Mathematicians) de 1954 à Amsterdam. Photographie T. Chotteau #1 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP.
Photographie T. Chotteau #1 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP. Photographie T. Chotteau #2 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP.
Photographie T. Chotteau #2 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP. Photographie T. Chotteau #3 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP.
Photographie T. Chotteau #3 Photographie collée sur plaque de plâtre prise par Thérèse Chotteau en 1992 d'une vitrine où étaient conservés les modèles mathématiques à l'IHP. PJ-L-001 Surface minimale à la courbe de poursuite.
PJ-L-001 Surface minimale à la courbe de poursuite. PJ-L-002 Écorché de la surface de Boy.
PJ-L-002 Écorché de la surface de Boy. PJ-L-003 Fonctions de Weierstrass.
PJ-L-003 Fonctions de Weierstrass. PJ-L-004
PJ-L-004
 PJ-L-005 Fractal cubique.
PJ-L-005 Fractal cubique.