-
 PJ-S-071
PJ-S-071 \(x^4+y^4+z^4-2(x^2y^2+y^2z^2+z^2x^2)+4x^2y^2z^2=0\)
\(x=\sin u\)
\(y=\sin v\)
\(z=\sin (u+v)\)
-
 PJ-S-070
PJ-S-070 \(y^9[(x^2+y^2+z^2)^2-4(x^2+z^2)]-16x^2z^2(y^2-1)=0\)
-
 PJ-S-069
PJ-S-069 \((x^2+y^2(x^2+y^2+z^2)=z(x^2+y^2)\)
-
 PJ-S-068
PJ-S-068 \(x^2y^2+y^2z^2+z^2x^2+2xyz=0\)
-
 PJ-S-067
PJ-S-067 \(x^2y^2+y^2z^2+z^2x^2-2xyz=0\)
-
 PJ-S-066
PJ-S-066
-
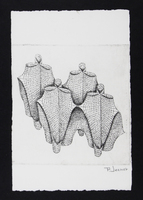 PJ-S-065
PJ-S-065
-
 PJ-S-064
PJ-S-064
-
 PJ-S-063
PJ-S-063 Fonctions sinus amplitude.
-
 PJ-S-062
PJ-S-062 Surface d'Apéry.
-
 PJ-S-061
PJ-S-061
-
 PJ-S-060
PJ-S-060 Théâtre du Gymnase.
-
 PJ-S-059
PJ-S-059
-
 PJ-S-058
PJ-S-058 Saint Séverin.
-
 PJ-S-057
PJ-S-057
-
 PJ-S-056
PJ-S-056
-
 PJ-S-055
PJ-S-055 \(z=x^2-y^2\)
\(w=z^2\)
-
 PJ-S-054
PJ-S-054 \(z(z^2+x^2+x)+y(z^2+xy+2xz)=0\)
-
 PJ-S-053
PJ-S-053 \(z^3+2z^2+zy^2+yx^2=0\)
-
 PJ-S-052
PJ-S-052 \(x^2+y^2)(z^2+1)-2(x^2y^2+z^2)=0\)
-
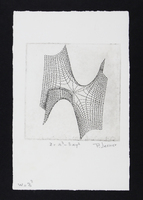 PJ-S-051
PJ-S-051 \(z=x^3-3xy^2\)
-
 PJ-S-050
PJ-S-050 \(x^3-3xy^2-3x^2-3y^2+z^2=0\)
-
 PJ-S-049
PJ-S-049 \(zx-y(x^2+y^2-1)=0\)
-
 PJ-S-048
PJ-S-048 \(z^3-3z-x^3+3xy^2=0\)
-
 PJ-S-047
PJ-S-047 \(z(x^5-10x^3y^2+5xy^4)-5x^4y+10x^2y^3-y^5-(x^2+y^2+z^2-1)^2=0\)
-
 PJ-S-046
PJ-S-046
-
 PJ-S-045
PJ-S-045
-
 PJ-S-044
PJ-S-044 \(z^2(x^2+y^2+z^2)-2z(x^2-y^2)-3(x^2+y^2)-10z^2+9=0\)
-
 PJ-S-043
PJ-S-043 \(x=3u+3uv^2-u^3\)
\(y=3v+3u^2v-v^3\)
\(z=3u^2-3v^2\)
-
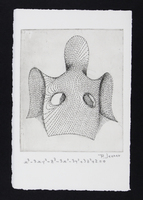 PJ-S-042
PJ-S-042 \(x^3-3xy^2-z^3-3x^2-3y^2+3z^2+2=0\)
-
 PJ-S-041
PJ-S-041
-
 PJ-S-040
PJ-S-040 \(x^3-3xy^2-z^3-3x^2-3y^2+4=0\)
-
 PJ-S-039
PJ-S-039 \(x^3-3xy^2-z^3+3z^2-3x^2-3y^2=0\)
-
 PJ-S-038
PJ-S-038 \(x^3-3xy^2-(z+3)(x^2+y^2)+z^3+3z^2+4\sqrt{2}=0\)
-
 PJ-S-037
PJ-S-037 \(x^3-3xy^2-z(x^2+y^2)-x^2-y^2+z^2=0\)
-
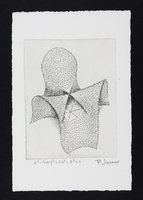 PJ-S-036
PJ-S-036 \(x^3-3xy^2+2z^2-z^3=0\)
-
 PJ-S-035
PJ-S-035 \((x-2)(xy+yz+zx)+z(y+z)^2=0\)
-
 PJ-S-034
PJ-S-034 \((x^2-4)(y+z)+z(y+z)^2-z^2(x-2)=0\)
-
 PJ-S-033
PJ-S-033 \([(z-2)^2-4y^2][(z-2)^2-4x^2]-2(x^2+y^2+z^2-3)^2=0\)
-
 PJ-S-032
PJ-S-032
-
 PJ-S-031
PJ-S-031
-
 PJ-S-030
PJ-S-030 Surface minimales au paraboles zéelles.
-
 PJ-S-029
PJ-S-029
-
 PJ-S-028
PJ-S-028
-
 PJ-S-027
PJ-S-027 \(x=\frac{1}{2}\log\frac{p^2+2p \sin 0+1}{p^2-2p \sin 0+1}\)
\(y=\frac{1}{2}\log\frac{p^2+2p \cos 0+1}{p^2-2p \cos 0+1}\)
\(z=arctg\frac{2p^2 \sin 20}{p^9-1}\)
-
 PJ-S-026
PJ-S-026 \(shx\ shy- \sin z=0\)
-
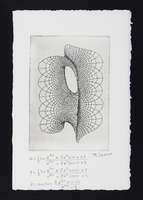 PJ-S-025
PJ-S-025 \(x=\frac{1}{2}Ln\frac{e^{2u}+2e^u \sin v+1}{e^{2u}-2e^u \sin v+1}\)
\(y=\frac{1}{2}Ln\frac{e^{2u} +2e^u \cos v+1}{e^{2u}-2e^u \cos v+1}\)
\(z=arctan \frac{2e^{2u} \sin 2v}{e^{4u}-1}\)
-
 PJ-S-024
PJ-S-024 \(x=u-\frac{e^{2u} \cos 2v}{2}\)
\(y=v-\frac{e^{2u} \sin 2v}{2}\)
\(z=2e^u \cos v^2\)
-
 PJ-S-023
PJ-S-023 \(w=x^2y^2z^2\)
-
 PJ-S-022
PJ-S-022
-
 PJ-S-021
PJ-S-021 \(w=e^u \cos v\)
\(x=e^u \sin v\)
\(y=u\)
\(z=v\)
-
 PJ-S-020
PJ-S-020 \(x=3uv^2-u^3+3u\)
\(y=3u^2-v^3+3v\)
\(z=3u^2-3v^2\)
 PJ-S-071 \(x^4+y^4+z^4-2(x^2y^2+y^2z^2+z^2x^2)+4x^2y^2z^2=0\) \(x=\sin u\) \(y=\sin v\) \(z=\sin (u+v)\)
PJ-S-071 \(x^4+y^4+z^4-2(x^2y^2+y^2z^2+z^2x^2)+4x^2y^2z^2=0\) \(x=\sin u\) \(y=\sin v\) \(z=\sin (u+v)\) PJ-S-070 \(y^9[(x^2+y^2+z^2)^2-4(x^2+z^2)]-16x^2z^2(y^2-1)=0\)
PJ-S-070 \(y^9[(x^2+y^2+z^2)^2-4(x^2+z^2)]-16x^2z^2(y^2-1)=0\) PJ-S-069 \((x^2+y^2(x^2+y^2+z^2)=z(x^2+y^2)\)
PJ-S-069 \((x^2+y^2(x^2+y^2+z^2)=z(x^2+y^2)\) PJ-S-068 \(x^2y^2+y^2z^2+z^2x^2+2xyz=0\)
PJ-S-068 \(x^2y^2+y^2z^2+z^2x^2+2xyz=0\) PJ-S-067 \(x^2y^2+y^2z^2+z^2x^2-2xyz=0\)
PJ-S-067 \(x^2y^2+y^2z^2+z^2x^2-2xyz=0\) PJ-S-066
PJ-S-066
 PJ-S-065
PJ-S-065
 PJ-S-064
PJ-S-064
 PJ-S-063 Fonctions sinus amplitude.
PJ-S-063 Fonctions sinus amplitude. PJ-S-062 Surface d'Apéry.
PJ-S-062 Surface d'Apéry. PJ-S-061
PJ-S-061
 PJ-S-060 Théâtre du Gymnase.
PJ-S-060 Théâtre du Gymnase. PJ-S-059
PJ-S-059
 PJ-S-058 Saint Séverin.
PJ-S-058 Saint Séverin. PJ-S-057
PJ-S-057
 PJ-S-056
PJ-S-056
 PJ-S-055 \(z=x^2-y^2\) \(w=z^2\)
PJ-S-055 \(z=x^2-y^2\) \(w=z^2\) PJ-S-054 \(z(z^2+x^2+x)+y(z^2+xy+2xz)=0\)
PJ-S-054 \(z(z^2+x^2+x)+y(z^2+xy+2xz)=0\) PJ-S-053 \(z^3+2z^2+zy^2+yx^2=0\)
PJ-S-053 \(z^3+2z^2+zy^2+yx^2=0\) PJ-S-052 \(x^2+y^2)(z^2+1)-2(x^2y^2+z^2)=0\)
PJ-S-052 \(x^2+y^2)(z^2+1)-2(x^2y^2+z^2)=0\) PJ-S-051 \(z=x^3-3xy^2\)
PJ-S-051 \(z=x^3-3xy^2\) PJ-S-050 \(x^3-3xy^2-3x^2-3y^2+z^2=0\)
PJ-S-050 \(x^3-3xy^2-3x^2-3y^2+z^2=0\) PJ-S-049 \(zx-y(x^2+y^2-1)=0\)
PJ-S-049 \(zx-y(x^2+y^2-1)=0\) PJ-S-048 \(z^3-3z-x^3+3xy^2=0\)
PJ-S-048 \(z^3-3z-x^3+3xy^2=0\) PJ-S-047 \(z(x^5-10x^3y^2+5xy^4)-5x^4y+10x^2y^3-y^5-(x^2+y^2+z^2-1)^2=0\)
PJ-S-047 \(z(x^5-10x^3y^2+5xy^4)-5x^4y+10x^2y^3-y^5-(x^2+y^2+z^2-1)^2=0\) PJ-S-046
PJ-S-046
 PJ-S-045
PJ-S-045
 PJ-S-044 \(z^2(x^2+y^2+z^2)-2z(x^2-y^2)-3(x^2+y^2)-10z^2+9=0\)
PJ-S-044 \(z^2(x^2+y^2+z^2)-2z(x^2-y^2)-3(x^2+y^2)-10z^2+9=0\) PJ-S-043 \(x=3u+3uv^2-u^3\) \(y=3v+3u^2v-v^3\) \(z=3u^2-3v^2\)
PJ-S-043 \(x=3u+3uv^2-u^3\) \(y=3v+3u^2v-v^3\) \(z=3u^2-3v^2\) PJ-S-042 \(x^3-3xy^2-z^3-3x^2-3y^2+3z^2+2=0\)
PJ-S-042 \(x^3-3xy^2-z^3-3x^2-3y^2+3z^2+2=0\) PJ-S-041
PJ-S-041
 PJ-S-040 \(x^3-3xy^2-z^3-3x^2-3y^2+4=0\)
PJ-S-040 \(x^3-3xy^2-z^3-3x^2-3y^2+4=0\) PJ-S-039 \(x^3-3xy^2-z^3+3z^2-3x^2-3y^2=0\)
PJ-S-039 \(x^3-3xy^2-z^3+3z^2-3x^2-3y^2=0\) PJ-S-038 \(x^3-3xy^2-(z+3)(x^2+y^2)+z^3+3z^2+4\sqrt{2}=0\)
PJ-S-038 \(x^3-3xy^2-(z+3)(x^2+y^2)+z^3+3z^2+4\sqrt{2}=0\) PJ-S-037 \(x^3-3xy^2-z(x^2+y^2)-x^2-y^2+z^2=0\)
PJ-S-037 \(x^3-3xy^2-z(x^2+y^2)-x^2-y^2+z^2=0\) PJ-S-036 \(x^3-3xy^2+2z^2-z^3=0\)
PJ-S-036 \(x^3-3xy^2+2z^2-z^3=0\) PJ-S-035 \((x-2)(xy+yz+zx)+z(y+z)^2=0\)
PJ-S-035 \((x-2)(xy+yz+zx)+z(y+z)^2=0\) PJ-S-034 \((x^2-4)(y+z)+z(y+z)^2-z^2(x-2)=0\)
PJ-S-034 \((x^2-4)(y+z)+z(y+z)^2-z^2(x-2)=0\) PJ-S-033 \([(z-2)^2-4y^2][(z-2)^2-4x^2]-2(x^2+y^2+z^2-3)^2=0\)
PJ-S-033 \([(z-2)^2-4y^2][(z-2)^2-4x^2]-2(x^2+y^2+z^2-3)^2=0\) PJ-S-032
PJ-S-032
 PJ-S-031
PJ-S-031
 PJ-S-030 Surface minimales au paraboles zéelles.
PJ-S-030 Surface minimales au paraboles zéelles. PJ-S-029
PJ-S-029
 PJ-S-028
PJ-S-028
 PJ-S-027 \(x=\frac{1}{2}\log\frac{p^2+2p \sin 0+1}{p^2-2p \sin 0+1}\) \(y=\frac{1}{2}\log\frac{p^2+2p \cos 0+1}{p^2-2p \cos 0+1}\) \(z=arctg\frac{2p^2 \sin 20}{p^9-1}\)
PJ-S-027 \(x=\frac{1}{2}\log\frac{p^2+2p \sin 0+1}{p^2-2p \sin 0+1}\) \(y=\frac{1}{2}\log\frac{p^2+2p \cos 0+1}{p^2-2p \cos 0+1}\) \(z=arctg\frac{2p^2 \sin 20}{p^9-1}\) PJ-S-026 \(shx\ shy- \sin z=0\)
PJ-S-026 \(shx\ shy- \sin z=0\) PJ-S-025 \(x=\frac{1}{2}Ln\frac{e^{2u}+2e^u \sin v+1}{e^{2u}-2e^u \sin v+1}\) \(y=\frac{1}{2}Ln\frac{e^{2u} +2e^u \cos v+1}{e^{2u}-2e^u \cos v+1}\) \(z=arctan \frac{2e^{2u} \sin 2v}{e^{4u}-1}\)
PJ-S-025 \(x=\frac{1}{2}Ln\frac{e^{2u}+2e^u \sin v+1}{e^{2u}-2e^u \sin v+1}\) \(y=\frac{1}{2}Ln\frac{e^{2u} +2e^u \cos v+1}{e^{2u}-2e^u \cos v+1}\) \(z=arctan \frac{2e^{2u} \sin 2v}{e^{4u}-1}\) PJ-S-024 \(x=u-\frac{e^{2u} \cos 2v}{2}\) \(y=v-\frac{e^{2u} \sin 2v}{2}\) \(z=2e^u \cos v^2\)
PJ-S-024 \(x=u-\frac{e^{2u} \cos 2v}{2}\) \(y=v-\frac{e^{2u} \sin 2v}{2}\) \(z=2e^u \cos v^2\) PJ-S-023 \(w=x^2y^2z^2\)
PJ-S-023 \(w=x^2y^2z^2\) PJ-S-022
PJ-S-022
 PJ-S-021 \(w=e^u \cos v\) \(x=e^u \sin v\) \(y=u\) \(z=v\)
PJ-S-021 \(w=e^u \cos v\) \(x=e^u \sin v\) \(y=u\) \(z=v\) PJ-S-020 \(x=3uv^2-u^3+3u\) \(y=3u^2-v^3+3v\) \(z=3u^2-3v^2\)
PJ-S-020 \(x=3uv^2-u^3+3u\) \(y=3u^2-v^3+3v\) \(z=3u^2-3v^2\)