-
 Cy-Dup-020
Cy-Dup-020 L'inversion de centre \( 0 \) et de rapport \( 1 \) est une transformation de l'espace qui échange tout point distinct de \( 0 \) avec un point de la même demi-droite issue de \( 0 \) et dont la distance à l'origine est l'inverse de celle du point de départ. Cette transformation jouit de la propriété de transformer les cercles en cercles, à condition toutefois de considérer les droites comme des cercles de rayon infini. Il en résulte que l'inverse d'un tore contient, comme le tore, quatre familles de cercles. Une telle surface s'appelle cyclide de Dupin.
Elles ont été découvertes par Charles Dupin en 1822. Selon la position du centre d'inversion par rapport au tore, l'aspect de la cyclide varie. Pour ce modèle (cyclide parabolique), le centre d'inversion est sur le tore.
Les cyclides de Dupin, comme les tores, sont des surfaces du 4ème degré.
-
 Cy-Dup-021
Cy-Dup-021 L'inversion de centre \( 0 \) et de rapport \( 1 \) est une transformation de l'espace qui échange tout point distinct de \( 0 \) avec un point de la même demi-droite issue de \( 0 \) et dont la distance à l'origine est l'inverse de celle du point de départ. Cette transformation jouit de la propriété de transformer les cercles en cercles, à condition toutefois de considérer les droites comme des cercles de rayon infini. Il en résulte que l'inverse d'un tore contient, comme le tore, quatre familles de cercles. Une telle surface s'appelle cyclide de Dupin.
Elles ont été découvertes par Charles Dupin en 1822. Selon la position du centre d'inversion par rapport au tore, l'aspect de la cyclide varie. Pour ce modèle (cyclide croisée interne), le tore est croisé, autrement dit, le cercle générateur coupe l'axe de révolution, et le centre d'inversion est à l'extérieur du tore.
Les cyclides de Dupin, comme les tores, sont des surfaces du 4ème degré.
-
 Cy-Dup-025
Cy-Dup-025 Cyclide du 3ème degré : noyau.
\(z(x^2+y^2+z^2-5z+4)-x^2-4y^2=0\)
-
 Cy-Dup-026
Cy-Dup-026 Cyclide du 3ème degré : collier ouvert.
\(z(x^2+y^2+z^2-10z+16)-8y^2=0\)
-
 Cy-Dup-027
Cy-Dup-027 Cyclides du 3ème degré : collier nul.
\(z(x^2+y^2+z^2-2z+1)-x^2=0\)
-
 Cy-Dup-028
Cy-Dup-028 Cyclide de 3ème degré.
\(z(x^2+y^2+z^2)+2(x^2-y^2)-16z=0\)
-
 Cy-Dup-030
Cy-Dup-030 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre.
Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
-
 Cy-Dup-031
Cy-Dup-031 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre.
Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
-
 Cy-Dup-032
Cy-Dup-032 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre.
Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
-
 Cy-Dup-033
Cy-Dup-033 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre.
Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
-
 Cy-Dup-034
Cy-Dup-034 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre.
Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
-
 Cy-Dup-035
Cy-Dup-035 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre.
Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
-
 Cy-Dup-036
Cy-Dup-036 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre.
Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
-
 Cy-Dup-037
Cy-Dup-037 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre.
Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
-
 Cy-Dup-038
Cy-Dup-038 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre.
Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
-
 Cy-Tor-001
Cy-Tor-001 Pénétration bitangente de la sphère et du tore (arrachement suivant deux cercles).
Tore arraché et solide commun.
-
 Cy-Tor-002
Cy-Tor-002 Pénétration bitangente de la sphère et du tore (arrachement suivant deux cercles).
Sphère arrachée.
-
 Cy-Tor-003
Cy-Tor-003 Cyclide. Cercles de Villarceau.
-
 Dactyle
Dactyle N°8189
-
 E001
E001 Levé de bâtiments.
Plan de la salle de travaux graphiques.
-
 E002
E002 Lavis.
Cylindres dépolis en projection verticale.
-
 E003
E003
-
 E004
E004
-
 E005
E005 Intersection de deux prismes. Solide commun.
-
 E006
E006 Intersection de deux cones.
-
 E007
E007 Intersection d'un cône et d'un cylindre ayant un plan tangent commun.
Spéciale B.
-
 E008
E008
-
 E009
E009 Spéciale B.
-
 E010
E010
-
 E011
E011
-
 E012
E012
-
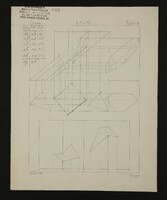 E013
E013 1e sciences.
-
 E014
E014 Deux cônes, plan tangent commun.
-
 E015
E015
-
 E016
E016 Perspective conique.
-
 E017
E017 Solide commun à deux prismes.
-
 E018
E018 Composition, pl. 6.
-
 E019
E019
-
 E020
E020 Cône de rév. et tore.
Composition.
Spé B.
-
 E021
E021 Intersection d'un hyperboloïde et d'un cône de révolution.
-
 E022
E022
-
 E023
E023 Composition.
-
 E024
E024
-
 E025
E025 Sphère et trièdre.
-
 E026
E026 Intersection d'une pyramide et d'une sphère.
-
 E027
E027
-
 E028
E028
-
 E029
E029 Math. Spéciales A.
-
 E030
E030 Cône et cylindre de révolution tangents en C, C'.
Sections par plan (LT,C,C').
-
 E031
E031
-
 E032
E032
-
 E033
E033
 Cy-Dup-020 L'inversion de centre \( 0 \) et de rapport \( 1 \) est une transformation de l'espace qui échange tout point distinct de \( 0 \) avec un point de la même demi-droite issue de \( 0 \) et dont la distance à l'origine est l'inverse de celle du point de départ. Cette transformation jouit de la propriété de transformer les cercles en cercles, à condition toutefois de considérer les droites comme des cercles de rayon infini. Il en résulte que l'inverse d'un tore contient, comme le tore, quatre familles de cercles. Une telle surface s'appelle cyclide de Dupin. Elles ont été découvertes par Charles Dupin en 1822. Selon la position du centre d'inversion par rapport au tore, l'aspect de la cyclide varie. Pour ce modèle (cyclide parabolique), le centre d'inversion est sur le tore. Les cyclides de Dupin, comme les tores, sont des surfaces du 4ème degré.
Cy-Dup-020 L'inversion de centre \( 0 \) et de rapport \( 1 \) est une transformation de l'espace qui échange tout point distinct de \( 0 \) avec un point de la même demi-droite issue de \( 0 \) et dont la distance à l'origine est l'inverse de celle du point de départ. Cette transformation jouit de la propriété de transformer les cercles en cercles, à condition toutefois de considérer les droites comme des cercles de rayon infini. Il en résulte que l'inverse d'un tore contient, comme le tore, quatre familles de cercles. Une telle surface s'appelle cyclide de Dupin. Elles ont été découvertes par Charles Dupin en 1822. Selon la position du centre d'inversion par rapport au tore, l'aspect de la cyclide varie. Pour ce modèle (cyclide parabolique), le centre d'inversion est sur le tore. Les cyclides de Dupin, comme les tores, sont des surfaces du 4ème degré. Cy-Dup-021 L'inversion de centre \( 0 \) et de rapport \( 1 \) est une transformation de l'espace qui échange tout point distinct de \( 0 \) avec un point de la même demi-droite issue de \( 0 \) et dont la distance à l'origine est l'inverse de celle du point de départ. Cette transformation jouit de la propriété de transformer les cercles en cercles, à condition toutefois de considérer les droites comme des cercles de rayon infini. Il en résulte que l'inverse d'un tore contient, comme le tore, quatre familles de cercles. Une telle surface s'appelle cyclide de Dupin. Elles ont été découvertes par Charles Dupin en 1822. Selon la position du centre d'inversion par rapport au tore, l'aspect de la cyclide varie. Pour ce modèle (cyclide croisée interne), le tore est croisé, autrement dit, le cercle générateur coupe l'axe de révolution, et le centre d'inversion est à l'extérieur du tore. Les cyclides de Dupin, comme les tores, sont des surfaces du 4ème degré.
Cy-Dup-021 L'inversion de centre \( 0 \) et de rapport \( 1 \) est une transformation de l'espace qui échange tout point distinct de \( 0 \) avec un point de la même demi-droite issue de \( 0 \) et dont la distance à l'origine est l'inverse de celle du point de départ. Cette transformation jouit de la propriété de transformer les cercles en cercles, à condition toutefois de considérer les droites comme des cercles de rayon infini. Il en résulte que l'inverse d'un tore contient, comme le tore, quatre familles de cercles. Une telle surface s'appelle cyclide de Dupin. Elles ont été découvertes par Charles Dupin en 1822. Selon la position du centre d'inversion par rapport au tore, l'aspect de la cyclide varie. Pour ce modèle (cyclide croisée interne), le tore est croisé, autrement dit, le cercle générateur coupe l'axe de révolution, et le centre d'inversion est à l'extérieur du tore. Les cyclides de Dupin, comme les tores, sont des surfaces du 4ème degré. Cy-Dup-025 Cyclide du 3ème degré : noyau. \(z(x^2+y^2+z^2-5z+4)-x^2-4y^2=0\)
Cy-Dup-025 Cyclide du 3ème degré : noyau. \(z(x^2+y^2+z^2-5z+4)-x^2-4y^2=0\) Cy-Dup-026 Cyclide du 3ème degré : collier ouvert. \(z(x^2+y^2+z^2-10z+16)-8y^2=0\)
Cy-Dup-026 Cyclide du 3ème degré : collier ouvert. \(z(x^2+y^2+z^2-10z+16)-8y^2=0\) Cy-Dup-027 Cyclides du 3ème degré : collier nul. \(z(x^2+y^2+z^2-2z+1)-x^2=0\)
Cy-Dup-027 Cyclides du 3ème degré : collier nul. \(z(x^2+y^2+z^2-2z+1)-x^2=0\) Cy-Dup-028 Cyclide de 3ème degré. \(z(x^2+y^2+z^2)+2(x^2-y^2)-16z=0\)
Cy-Dup-028 Cyclide de 3ème degré. \(z(x^2+y^2+z^2)+2(x^2-y^2)-16z=0\) Cy-Dup-030 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
Cy-Dup-030 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre. Cy-Dup-031 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
Cy-Dup-031 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre. Cy-Dup-032 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
Cy-Dup-032 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre. Cy-Dup-033 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
Cy-Dup-033 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre. Cy-Dup-034 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
Cy-Dup-034 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre. Cy-Dup-035 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
Cy-Dup-035 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre. Cy-Dup-036 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
Cy-Dup-036 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre. Cy-Dup-037 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
Cy-Dup-037 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre. Cy-Dup-038 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre.
Cy-Dup-038 Reprenant la question des cyclides en 1864, Gaston Darboux introduit une classe remarquable de surfaces du quatrième degré, appelées depuis cyclides de Darboux, qui contient en particulier les cyclides de Dupin. Ces surfaces jouissent de la propriété de contenir six familles de cercles, et même dix si on compte les cercles imaginaires. Les cyclides de Dupin correspondent au cas où certaines familles coïncident pour n’en former plus que quatre. Cette série de neuf modèles en bois dûs à Caron, représente différentes cyclides de Darboux. La partie en bois correspond au huitième de la surface située dans l’octant matérialisé par le trièdre sur lequel figure l’équation. On reconstitue l’ensemble de la surface au moyen des symétries par rapport aux plans du trièdre. Cy-Tor-001 Pénétration bitangente de la sphère et du tore (arrachement suivant deux cercles). Tore arraché et solide commun.
Cy-Tor-001 Pénétration bitangente de la sphère et du tore (arrachement suivant deux cercles). Tore arraché et solide commun. Cy-Tor-002 Pénétration bitangente de la sphère et du tore (arrachement suivant deux cercles). Sphère arrachée.
Cy-Tor-002 Pénétration bitangente de la sphère et du tore (arrachement suivant deux cercles). Sphère arrachée. Cy-Tor-003 Cyclide. Cercles de Villarceau.
Cy-Tor-003 Cyclide. Cercles de Villarceau. Dactyle N°8189
Dactyle N°8189 E001 Levé de bâtiments. Plan de la salle de travaux graphiques.
E001 Levé de bâtiments. Plan de la salle de travaux graphiques. E002 Lavis. Cylindres dépolis en projection verticale.
E002 Lavis. Cylindres dépolis en projection verticale. E003
E003
 E004
E004
 E005 Intersection de deux prismes. Solide commun.
E005 Intersection de deux prismes. Solide commun. E006 Intersection de deux cones.
E006 Intersection de deux cones. E007 Intersection d'un cône et d'un cylindre ayant un plan tangent commun. Spéciale B.
E007 Intersection d'un cône et d'un cylindre ayant un plan tangent commun. Spéciale B. E008
E008
 E009 Spéciale B.
E009 Spéciale B. E010
E010
 E011
E011
 E012
E012
 E013 1e sciences.
E013 1e sciences. E014 Deux cônes, plan tangent commun.
E014 Deux cônes, plan tangent commun. E015
E015
 E016 Perspective conique.
E016 Perspective conique. E017 Solide commun à deux prismes.
E017 Solide commun à deux prismes. E018 Composition, pl. 6.
E018 Composition, pl. 6. E019
E019
 E020 Cône de rév. et tore. Composition. Spé B.
E020 Cône de rév. et tore. Composition. Spé B. E021 Intersection d'un hyperboloïde et d'un cône de révolution.
E021 Intersection d'un hyperboloïde et d'un cône de révolution. E022
E022
 E023 Composition.
E023 Composition. E024
E024
 E025 Sphère et trièdre.
E025 Sphère et trièdre. E026 Intersection d'une pyramide et d'une sphère.
E026 Intersection d'une pyramide et d'une sphère. E027
E027
 E028
E028
 E029 Math. Spéciales A.
E029 Math. Spéciales A. E030 Cône et cylindre de révolution tangents en C, C'. Sections par plan (LT,C,C').
E030 Cône et cylindre de révolution tangents en C, C'. Sections par plan (LT,C,C'). E031
E031
 E032
E032
 E033
E033